Помогите пожалуйста. Я во вообще не могу понять как решить эту задачу.
Ответы
Ответ:
Объяснение:
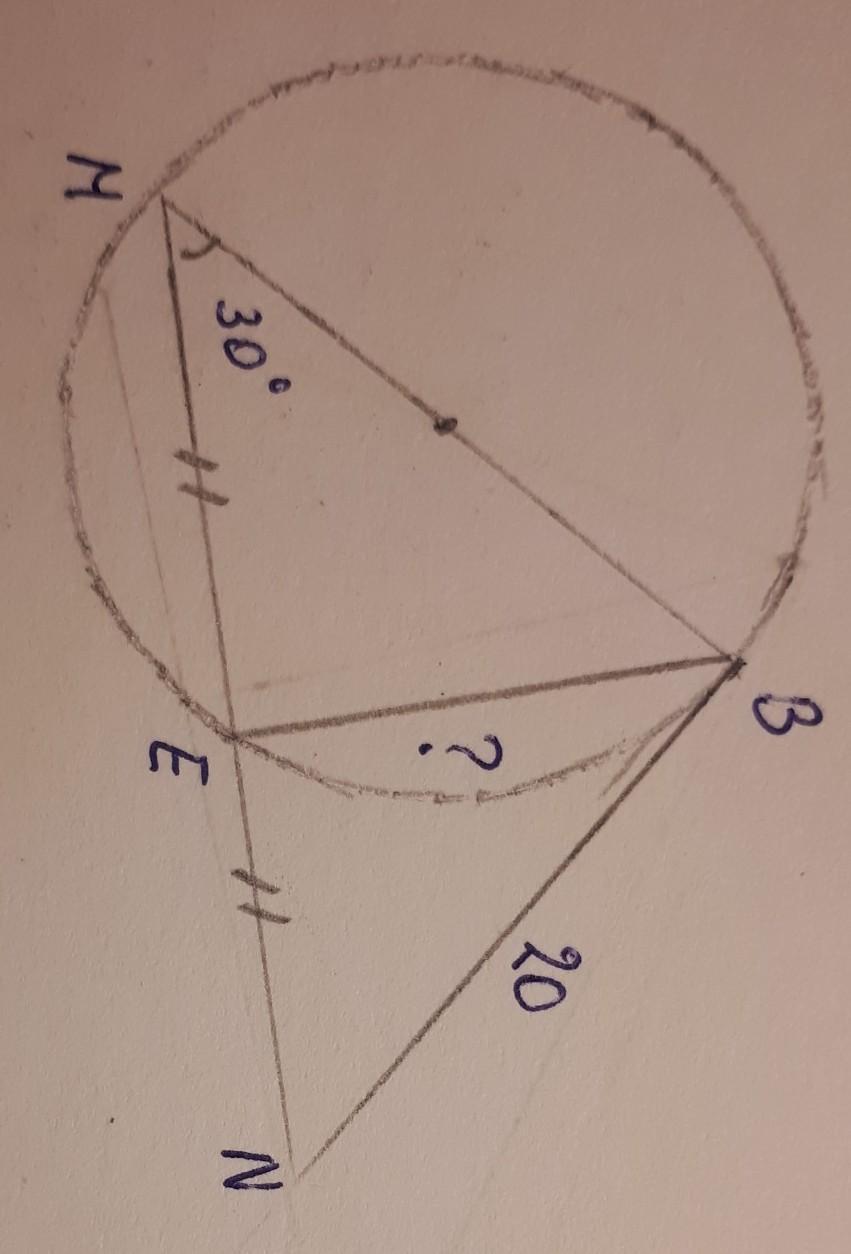
Если ВN - касательная и т.В принадлежит диаметру этой окружности, то
ВN ⊥МВ, то есть ΔМВN - прямоугольный,∠В=90*. Тогда ВN - катет против угла 30*⇒МN = 2ВN , МN =2×20=40
ВЕ - медиана ΔМВN ( так как по условию МЕ=ЕN ), проведенная из угла 90*, тогда ВЕ=1/2МN =40:2=20
ВЕ=40
Ответ: ВЕ=20см
Объяснение: так как ВN касательная, то диаметр ВМ с ней образуют прямой угол 90°. Из этого следует что ∆MBN-прямоугольный с катетами ВМ и BN. По свойствам угла 30°, катет, лежащий напротив него равен половине гипотенузы, значит гипотенуза МN=20×2=40см. Так как медиана делит гипотенузу пополам, то ME=EN=20см. Если угол М= 30°, то угол N= 90-30=60°. Рассмотрим ∆BEN. B нём известны 2 стороны и угол и теперь найдём по теореме косинусов ВЕ:
ВЕ²=EN²+BN²-2×EN×BN×cosN
BE²=20²+20²-2×20×20×cos60°=
=400+400-2×400×½=800-800×½=
=800-400=400; BE²=400; BE=√400=20см;. ВЕ=20см
Также, медиана, проведённая из прямого угла к гипотенузе, равна её половине.
Т.е ВЕ=40÷2=20см