Предмет: Геометрия,
автор: arishabanana
Меньшая сторона параллелограмма равна 20 см. Высота, проведённая из вершины тупого угла, делит большую сторону параллелограмма на отрезки 12 см и 15 см, считая от вершины острого угла. Найдите площадь параллелограмма. Ответ дайте в квадратных сантиметрах.
Пожалуйста))
Ответы
Автор ответа:
15
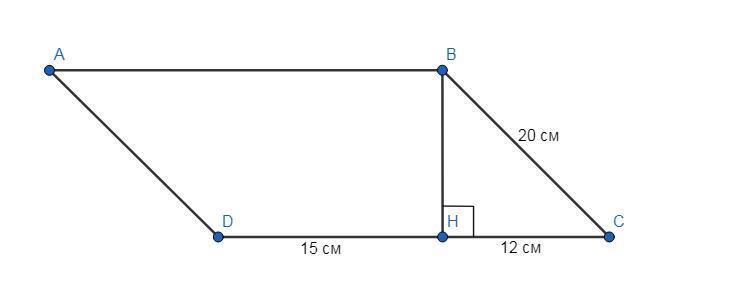
Дано:
ABCD - параллелограмм.
ВС - меньшая сторона = 20 см.
ВН - высота.
СН = 12 см.
НD = 15 см.
Найти:
S(ABCD) = ?
Решение:
1) Рассмотрим прямоугольный ΔBHC. По теореме Пифагора :
BH = 16 см.
2) Площадь параллелограмма равна произведению стороны (основания) и высоты, проведённой к этой стороне.
В данном случае за основание примем сторону DC.
DC = HD+CH = 15 см+12 см = 27 см.
Высота, проведённая к этому основанию - BH = 16 см.
Тогда :
S(ABCD) = 432 см^2.
Ответ: 432 см^2.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Sapfirchik80
Предмет: Математика,
автор: strella255
Предмет: География,
автор: koneva90
Предмет: Химия,
автор: diank3txjLelegra
Предмет: Математика,
автор: Irauser