Предмет: Алгебра,
автор: dimirycomovalov
Помогите пожалуйста сделать!!!
Приложения:
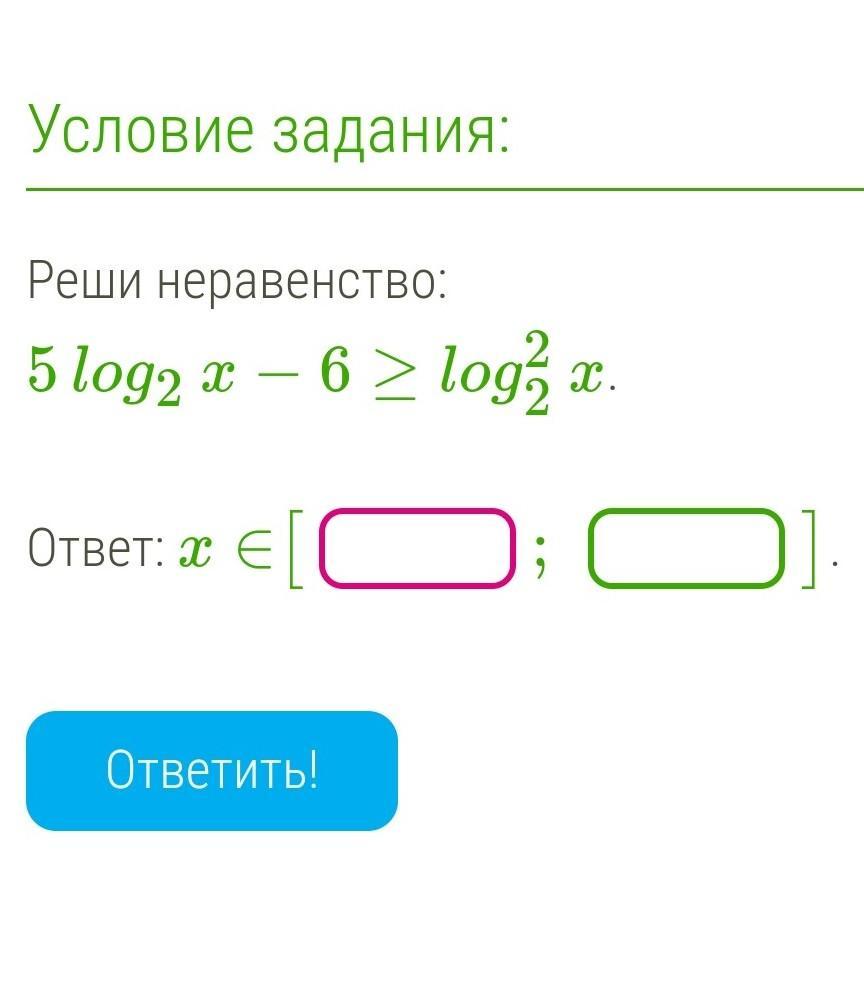
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: х>0.
Пусть log₂x=t ⇒
-∞__+__4__-__8__+__+∞
x(-∞;4)U(8;+∞).
Похожие вопросы
Предмет: География,
автор: vasiok62
Предмет: Русский язык,
автор: ололол0
Предмет: Английский язык,
автор: Shevkina86
Предмет: Математика,
автор: Gost1111
Предмет: Алгебра,
автор: morozovaKi