Предмет: Алгебра,
автор: t0509271098
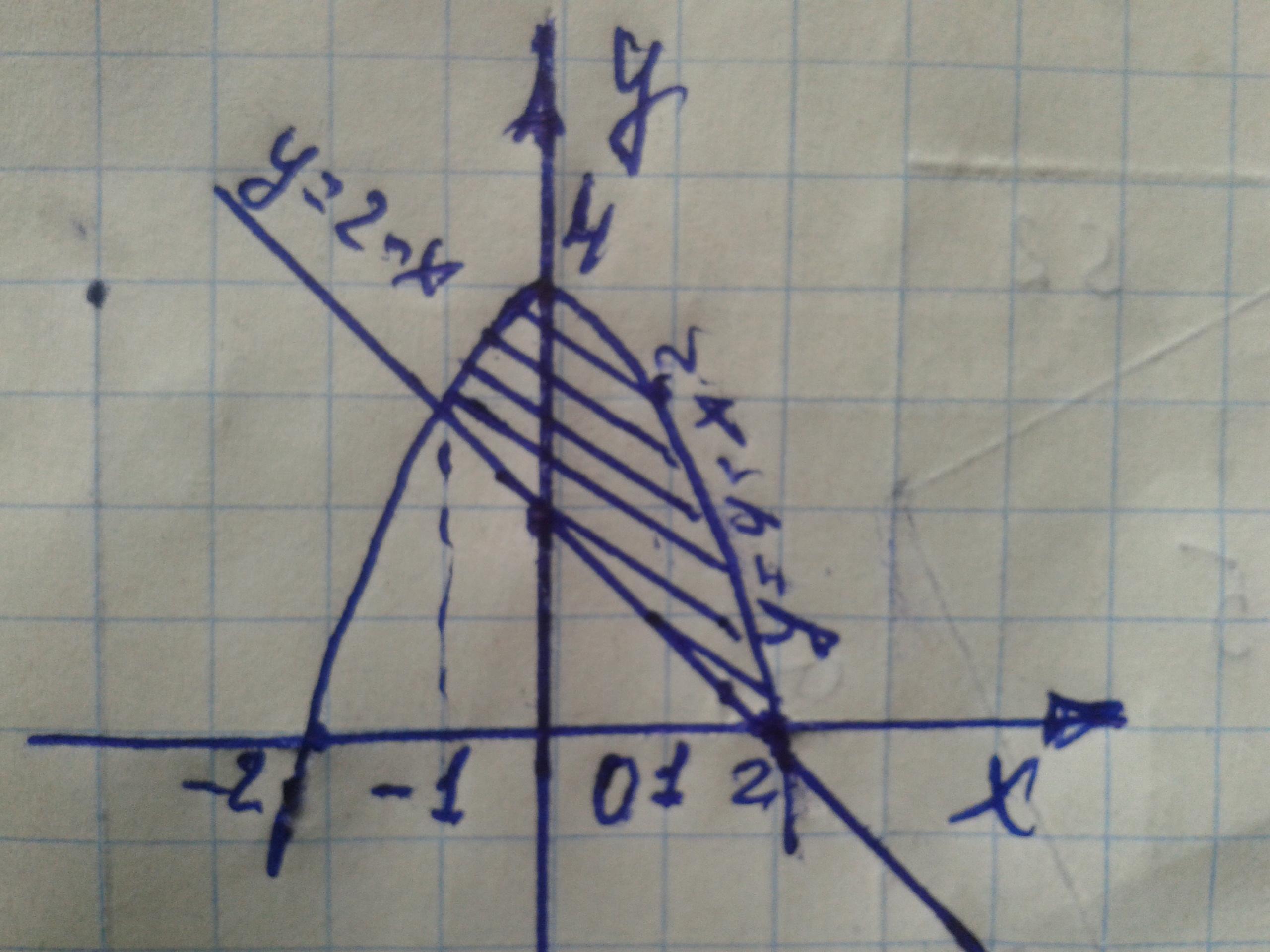
Обчислити площу фігури обмеженої параболою у= 4 - х^2 і прямою у=2-х
Это срочно! Если можно. С рисунком
Ответы
Автор ответа:
8
Ответ: S=4,5 кв. ед.
Объяснение:
y=4-x² y=2-x S=?
4-x²=2-x
x²-x-2=0 D=9 √D=3
x₁=-1 x₂=2
Приложения:
t0509271098:
это грани, а площадь?
Немного задержался с ответом.
Сейчас будет чертёж.
Похожие вопросы
Предмет: Алгебра,
автор: kachalinaiulia
Предмет: Обществознание,
автор: Ksuuha2001
Предмет: Русский язык,
автор: grigori2002
Предмет: Математика,
автор: Алжн111