Предмет: Алгебра,
автор: 25hjoerf10
Найти производную функции.
Нужен ответ, как на 2-ом фото.
Приложения:

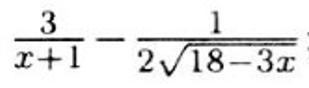
zaloznijroman2:
помоги мне с вопросом в моем профиле пожалуйста
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Спасибо большое!!!
Удачи.
и мне помогите вопрос в моем профиле пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: nastia80
Предмет: Русский язык,
автор: alexa010101
Предмет: Русский язык,
автор: baraboljka
Предмет: Литература,
автор: litvinova45