Предмет: Математика,
автор: gor346saha
Помогите пожалуйста с высшей математикой
Приложения:
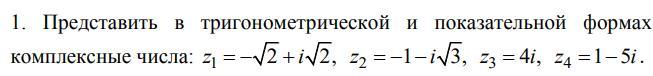
Ответы
Автор ответа:
2
z1 = -√2 + i*√2
тригонометрическая форма:
находим модуль
|z1| =
a<0 b>0 (вторая координатная четверть)
находим аргумент
arg(z) = π + arctg(b/a)
arg(z) = π + arctg(√2/-√2) = π - π/4 = 3π/4
⇒ z1 = 2(cos(3π/4) + i*sin(3π/4))
показательная форма:
z = |z| = 2*e^((3π/4)*i)
z2 = -1 - i*√3
находим модуль:
|z2| =
a<0 b>0 (вторая коорд. четверть)
arg(z2) = π + arctg(-√3/-1) = π + π/3 = 4π/3
⇒ z2 = 2(cos(4π/3) + i*sin(4π/3))
показательная форма:
z2 = 2*e^((i*4π/3))
z3 = 4i
|z3| = 4
a=0 b>0 (ось y)
arg(z3) = π/2 (представь тригонометрический круг)
⇒ z3 = 4(cos(π/2) + i*sin(π/2))
z3 = 4*e^(i*π/2)
z4 = 1 - 5i
|z4| =
a>0 b<0 (4 коорд. четверть)
arg(z4) = arctg(-5/1) = -arctg5
⇒ z4 = (cos(-arctg5) + i*sin(-arctg5))
z4 = *e^(i*(-arctg5))
Похожие вопросы
Предмет: Математика,
автор: 777IO8YT
Предмет: Русский язык,
автор: natdedova
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: saaiskavikaya
Предмет: Литература,
автор: machapismichenko