Question

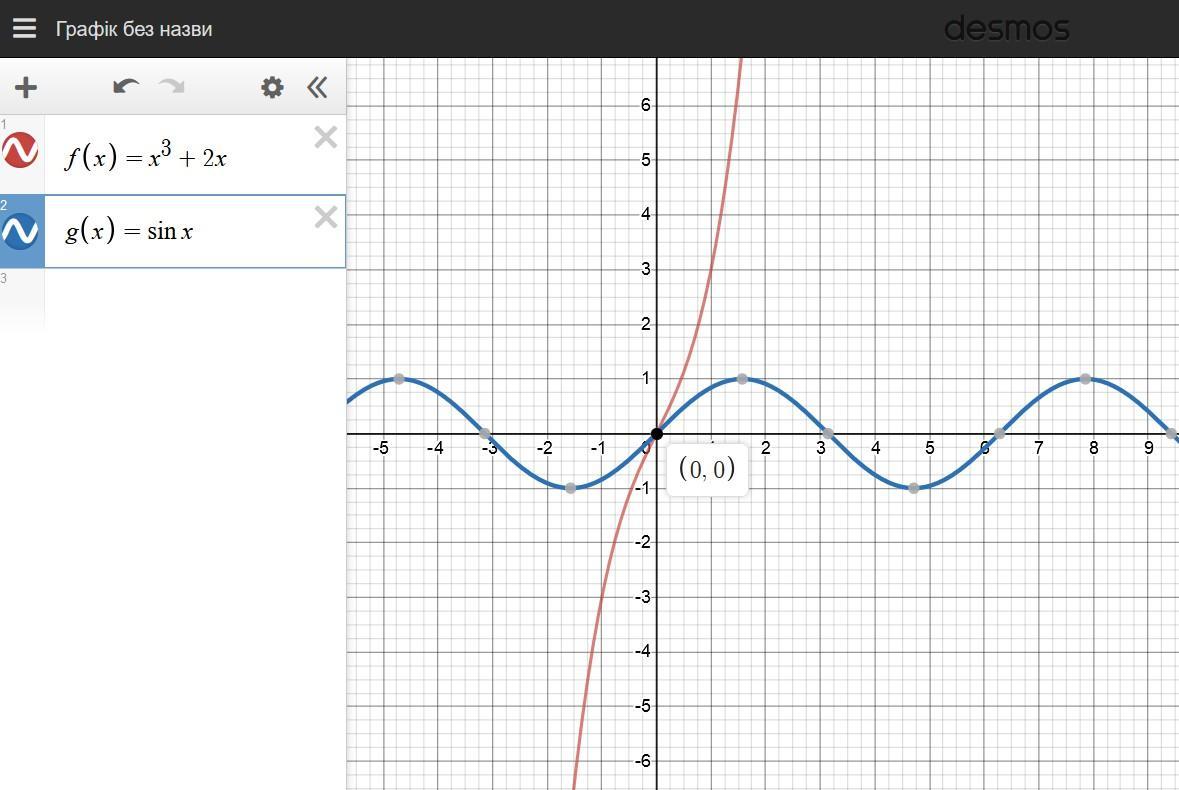
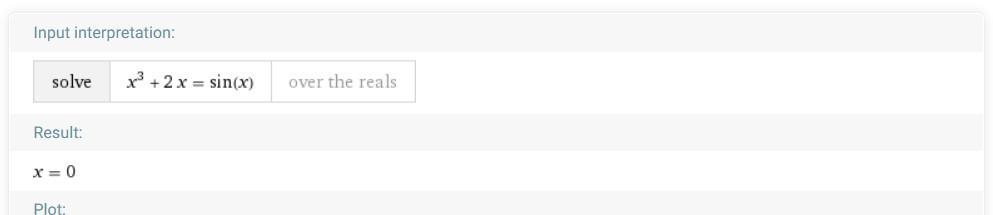
Розв'яжіть рівняння (x^3)+2x=sinx

Answer 1

$x^3+2x=\sin x$

Перший корінь одразу видно: це 0 (бо $\sin 0=0$).

Доведемо, що інших коренів немає. Щоб їх не було, функція $f(x)=x^3+2x$ має рости (або спадати — тут це неважливо, бо обидві функції непарні) швидше, ніж функція $g(x)=\sin x$ на всій області визначення (тобто її похідна має бути більшою) Знайдемо похідні обох функцій:

$f'(x)=3x^2+2\\g'(x)=\cos x$

Доведемо, що $\forall x: f'(x) > g'(x)$, тобто $3x^2+2> \cos x$. Це випливає з того, що $\cos x \leqslant 1$ (за означенням косинуса), а $3x^2+2>1$ (доведемо це):

$3x^2+2>1\\3x^2>-1\\x^2>-\dfrac{1}{3}$

Квадрат виразу не може бути від'ємним на множині дійсних чисел, тому нерівність доведено.

Відповідь: $x=0$.