Question

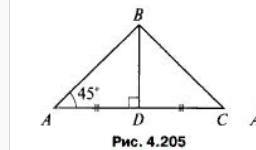
Дано: АС = 5 см .
Найти: расстояние от точки В до прямой АС (рис. 4.205)

Answer 1

Дано:

∆АВС.

∠А = 45°

BD - высота, медиана.

АС = 5 см.

Найти:

Расстояние от В до АС.

Решение.

∆ABD и ∆CBD - прямоугольные.(так как BD - высота)

Рассмотрим эти треугольники.

AD = DC, по условию

BD - общая сторона.

=> ∆ABD = ∆CBD, по катетам.

=> ∆АВС - равнобедренный.

Сумма острых углов прямоугольного треугольника равна 90°

=> ∠ABD = ∠CBD = 90 - 45 = 45°(если треугольник равнобедренный то высота, проведённая из основания к вершине треугольника, является ещё и биссектрисой)

=> ∠АВС - прямой (90°)

Медиана, проведённая из прямого угла к гипотенузе равна половине гипотенузы.

=> ВD = 5 ÷ 2 = 2,5 см.

Ответ: 2,5 см.