Question

Бічна сторона рівнобедреного трикутника дорівнює 34 см, а висота, проведена до основи - 30 см. Знайти площу трикутника.

Answer 1

Дано:

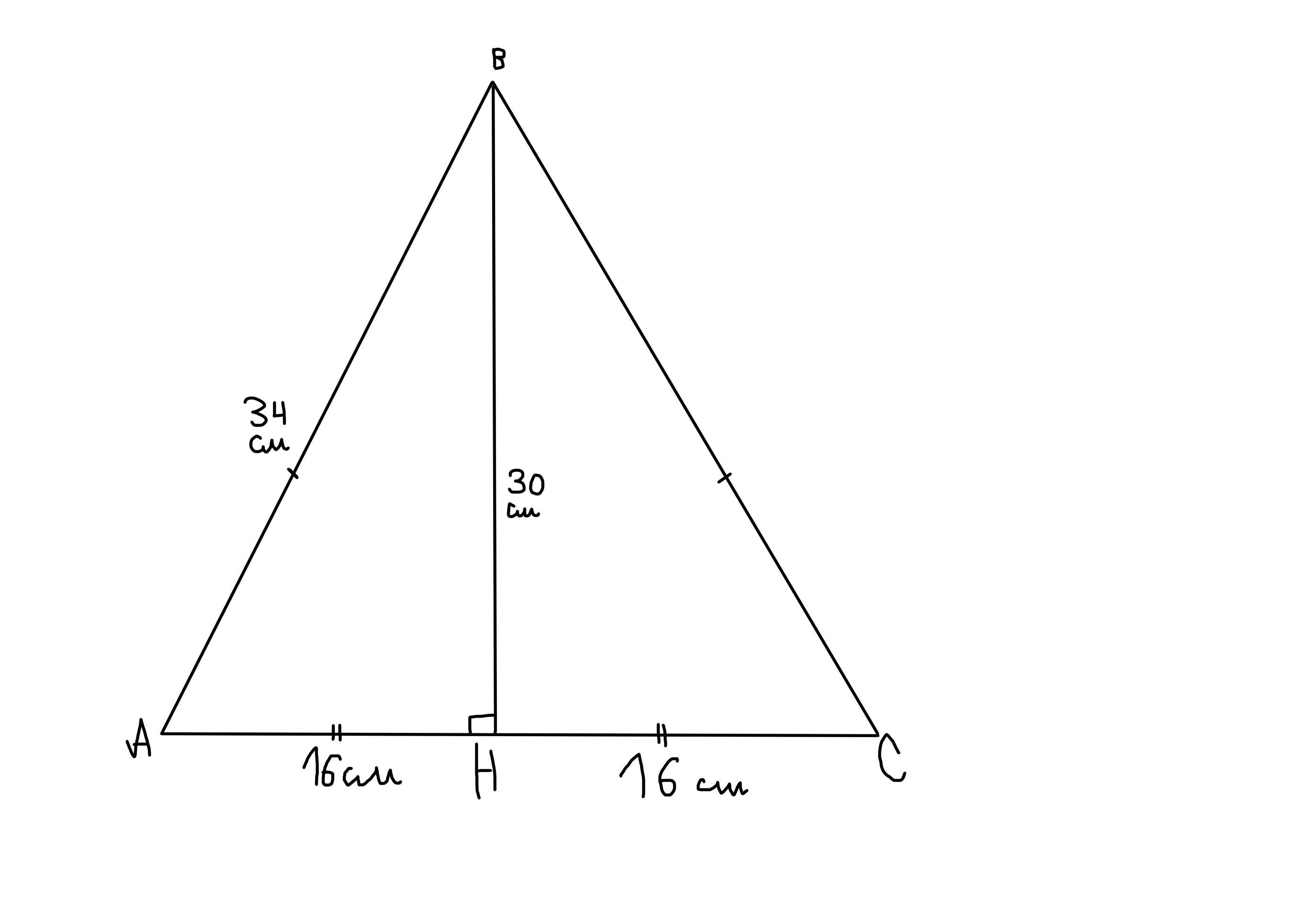
ΔАВС - равнобедренный (АВ = ВС, АС - основание).

АВ = 34 см.

ВН - высота = 30 см.

Найти:

S(ΔABC) = ?

Решение:

1. Так как BH - высота, проведённая к основанию равнобедренного треугольника, то ВН - медиана и биссектриса. Тогда АН = НС.

2. Рассмотрим ΔАВН прямоугольный.

По теореме Пифагора :

$AB^{2} -BH^{2} =AH^{2} \\34^{2} -30^{2} =AH^{2}\\1156-900 =AH^{2}\\AH^{2}=256\\AH = 16$

АН = 16 см.

Тогда всё основание АС = 16 см*2 = 32 см.

3. Площадь треугольника равна половине произведения его высоты на сторону, к которой проведена эта высота.

Следовательно :

$S(ABC) = 0,5*AC*BH\\S(ABC) = 0,5*32*30\\S(ABC) = 480$

S(ΔABC) = 480 см^2.

Ответ: 480 см^2.