помогите, очень прошу...
даю много баллов

Ответы
Ответ:
4) формула нахождения радиуса вписанной окружности в правильный треугольник:
r=a/2√3
где a - сторона
подставляем: r=2√3/2√3 = 1
5) по той же формуле, просто выражаем a:
a=r*2√3
подставляем наш радиус:
a= 2√3*2√3/3= 4
6) жаль нет возможности нарисовать рисунок, но:
KB=LB=5,5
LC=CM = 9,5
AM=AK=10
Найдем стороны:
AB= AK+KB=10+5,5= 15,5
BC= BL+LC = 5,5+9,5= 15
CA= AM+MC= 10+9,5= 19,5
P= AB+BC+CA= 15,5+15+19,5= 50 cm
7) (прикрепил рисунок)
По рисунку видно, что радиус вписанной окружности равен кусочку BK т.к радиус в точке касания создаёт перпендикуляр, и в прямоугольном треугольнике мы получаем квадрат, => r= BK = 13
8) Треугольник прямоугольный, известны 2 катета, найдем гипотенузу AB:
По теореме Пифагора:
AB= √(AC²+BC²)= √(15²+8²)= 17
Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле:
r=(a+b-c)/2
где a и b - катеты, а c - гипотенуза
подставляем:
r= (15+8-17)/2 = 3
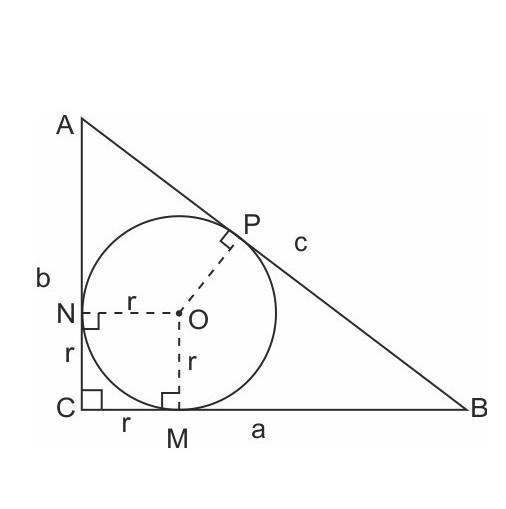
9) Рассмотрим универсальный рисунок, и будем работать по нему:
AB=15 значит BP=BM=x, а PA=AN=15-x
CM=CN=r=3
AC= 15-x+3 =18-x
CB= 3+x
По теореме Пифагора:
AC²+CB²=AB²
подставляем все что известно:
(18-x)²+(3+x)²=15²
При разложении получили квадратное уравнение:
x²-15x+54=0
по т Виета:
x1=6
x2=9
К сожалению, тут оба x являются истинными.
найдем периметр относительно x1:
P=AC+CB+AB=12+9+15=36
относительно x2:
P=AC+CB+AB=9+12+15=36 =>
=> периметр равен 36 см
Если есть вопросы, задавайте в комментариях