Предмет: Математика,
автор: lianaunicorn16
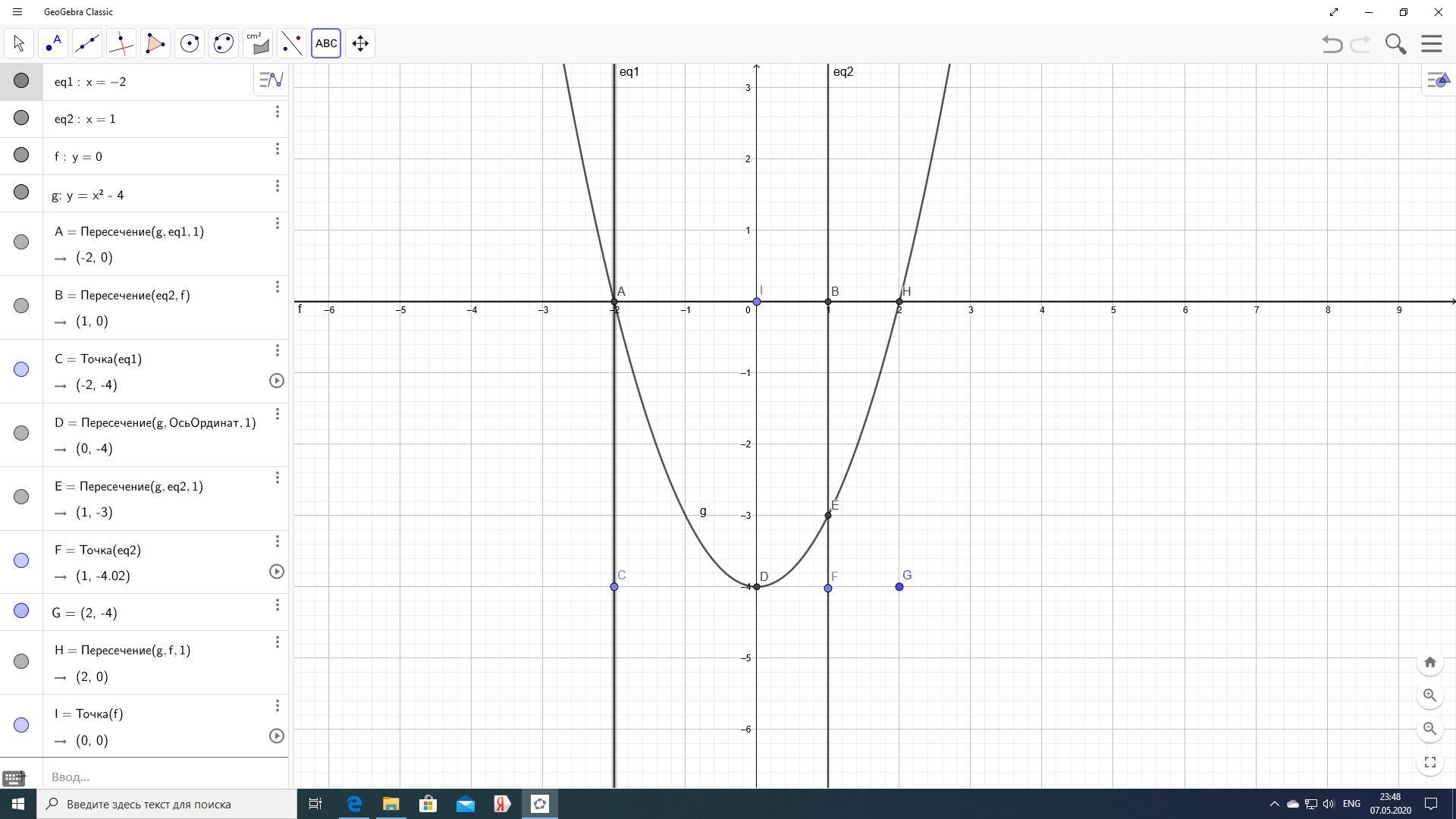
Вычислите площадь фигуры с ограниченными линиями
y=x^2-4, y=0, x=-2, x=1
nv26353:
помимо линий, здесь ещё ограниченная я ✌️
P.S приколюха в том, что надо с интегралами решать
Ответы
Автор ответа:
1
Ответ: 9
Пошаговое объяснение:
Найти S ADEB
S ADI = 2/3 * 4 * 2 (Парабола делит площадь прямоугольника от вершины до точки в отношении 2:1) = 16/3
S до DE = 2/3 *1 = 2/3
S после DE до IB = 1*3 = 3
Общая площадь - 16/3 + 2/3 + 3 = 6 + 3 = 9
ВОТ ИНТЕГРАЛОМ:
Рассмотрим интеграл от -2 до 1 функции -x^2+4 (Искомая площадь равна такой)
Получаем -x^3/3+4x от -2 до 1
Подставим -2:
8-8=0
Подставим 1:
-1-8=-9
Вычтем из 1 значения второе.
0- -9=9
ОТВЕТ:9
Приложения:
а можно с интегралами?
лучше с интегралом конечно)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: lnm0608
Предмет: Русский язык,
автор: sacha2580
Предмет: География,
автор: Endschpil