Предмет: Алгебра,
автор: hahaha000
Решите уравнение. Срочно
Приложения:
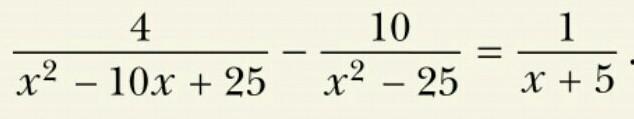
Ответы
Автор ответа:
1
Ответ:
9
Объяснение:
Найдем ОДЗ:
]
т.к ОДЗ мы нашли, то можем отбросить знаменатель.
Домножим на -1:
D=16+180=196
-5 не подходит по ОДЗ!
Подходит корень 9!
hahaha000:
Спасибо тебе огромное)
пожалуйста )
Можно попросить вас помочь мне с похожим примером?
Похожие вопросы
Предмет: Другие предметы,
автор: Alisa13kiska
Предмет: Другие предметы,
автор: SauleKuzhakova
Предмет: Английский язык,
автор: NastyaSOS
Предмет: Математика,
автор: tanynaever3adolych7