Question

Объясните пожалуйста, как решить данный пример: $cos^{2} x\ \textgreater \ \frac{3}{4}$

Answer 1

$\cos^{2} x>\dfrac{3}{4}$

$\cos^{2} x-\dfrac{3}{4}>0$

$\left(\cos x-\dfrac{\sqrt{3} }{2}\right)\left(\cos x+\dfrac{\sqrt{3} }{2}\right)>0$

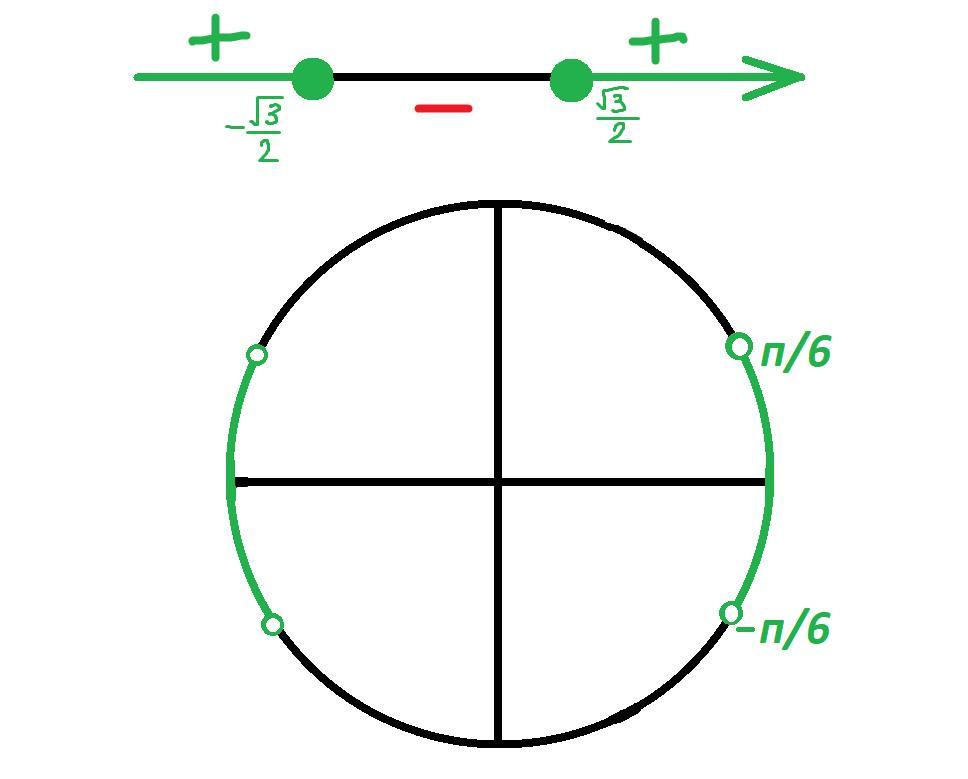
Решая неравенство методом интервалов относительно косинуса получим:

$\cos x\in\left(-\infty;\ -\dfrac{\sqrt{3} }{2}\right)\cup\left(\dfrac{\sqrt{3} }{2};\ +\infty\right)$

Учитывая, что косинус принимает значения на отрезке от -1 до 1, окончательно получим:

$\cos x\in\left[-1;\ -\dfrac{\sqrt{3} }{2}\right)\cup\left(\dfrac{\sqrt{3} }{2};\ 1\right]$

Отмечая решения на числовой окружности, получим:

$x\in\left(-\dfrac{\pi}{6}+\pi n;\ \dfrac{\pi }{6}+\pi n\right),\ n \in \mathbb{Z}$