Question

Окружность, вписана в треугольник со сторонами 5, 5 и 3. Найдите расстояние между точками ее касания с боковыми сторонами этого треугольника.

Answer 1

Ответ: 2,1 (ед. длины)

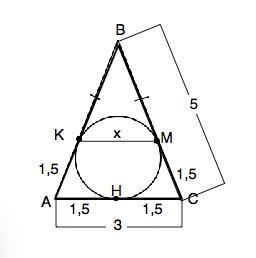
Объяснение: Пусть окружность вписана в ∆ АВС. Точки касания на боковых сторонах К и М, на основании Н. Искомое расстояние - КМ-  равно длине отрезка, который соединяет эти точки. .

Т.к. ∆ АВС равнобедренный ( стороны 5, 5 и 3), АН=СН=3:2=1,5

 Отрезки касательных, проведенных из одной точки к окружности, равны

АК=АН=СН=СМ=1,5 =>

КВ=МВ=5-1,5=3,5

∆ КВМ и ∆ АВС подобны по общему углу В и пропорциональным боковым сторонам .k=ВМ:ВС=0,7 =>

КМ=АС•k =3•0,7=2,1 (ед. длины)