Предмет: Алгебра,
автор: koshka5irenka
Помогите, пожалуйста, найти производную функции y=ln tg(2x+1)
Приложения:
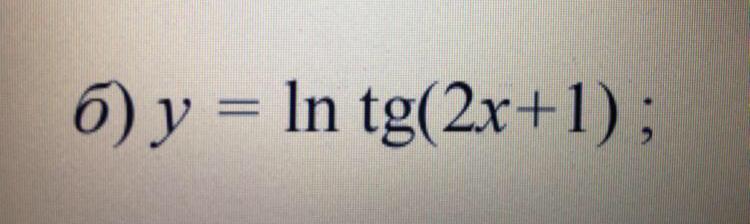
Ответы
Автор ответа:
3
Похожие вопросы
Предмет: Другие предметы,
автор: len76chik
Предмет: Русский язык,
автор: yagodamarina
Предмет: Другие предметы,
автор: olyateterina
Предмет: Математика,
автор: swordsmanplay
Предмет: Математика,
автор: shcolnikow