Предмет: Алгебра,
автор: solomiahruba5
Даю много баллов,нужно найти неопределенный интеграл
Приложения:
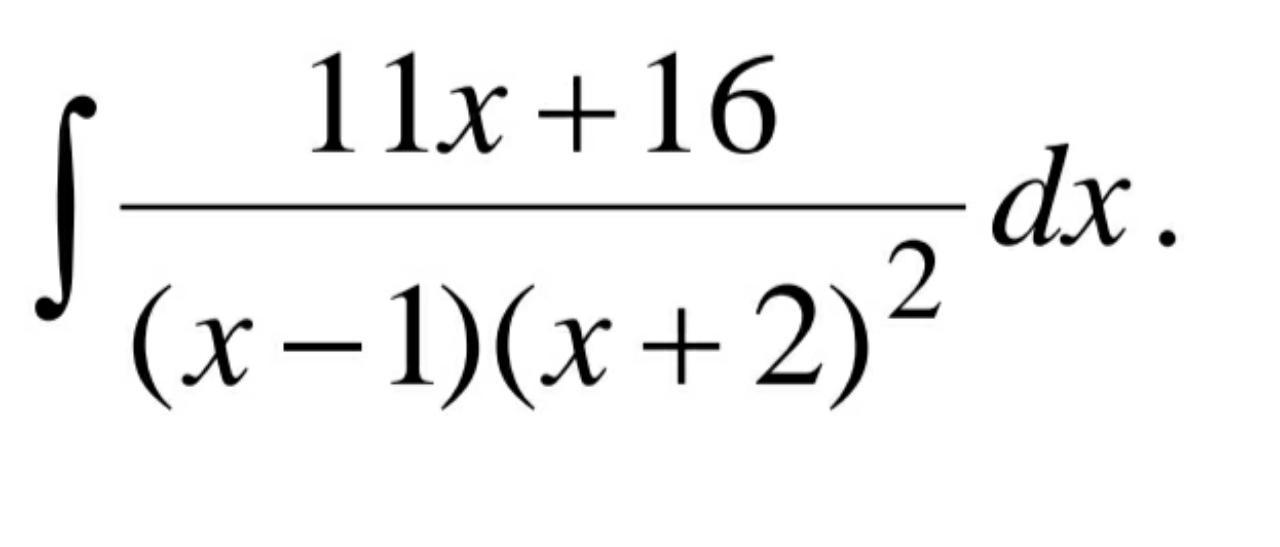
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Пусть u=x+2 ⇒ du=dx
Пусть u=x+2 ⇒ du=dx
Пусть u=x-1 ⇒ du=dx
⇒
Похожие вопросы
Предмет: Русский язык,
автор: АлеЧКАаАА
Предмет: Русский язык,
автор: zhanars2013
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: imunaline
Предмет: Математика,
автор: Dav20