Предмет: Алгебра,
автор: slonikkaterina21
помогите вычислить пожалуйста
Приложения:
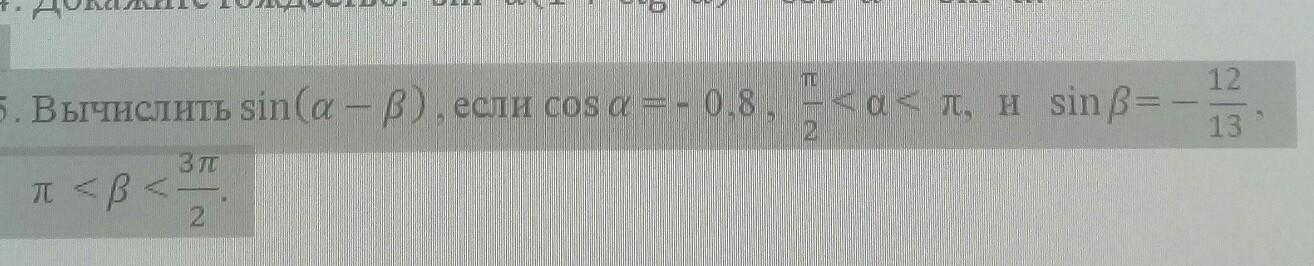
Ответы
Автор ответа:
1
α - угол второй четверти значит Sinα > 0 .
β - угол третьей четверти значит Cosβ < 0 .
Похожие вопросы
Предмет: Русский язык,
автор: Даша978
Предмет: Қазақ тiлi,
автор: 00ю
Предмет: Русский язык,
автор: киллео
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: dasha2042