Предмет: Алгебра,
автор: kent2121
Помогите жду решения хотя бы что-то полностью или хотя бы половину расписать решения даю много баллов
Приложения:
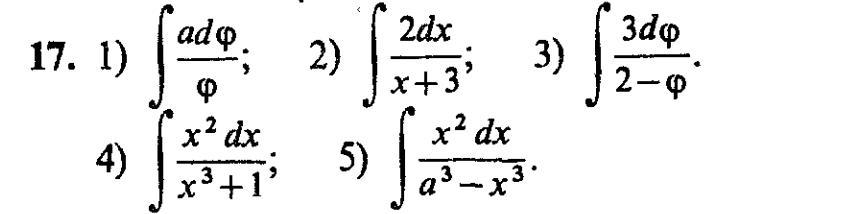
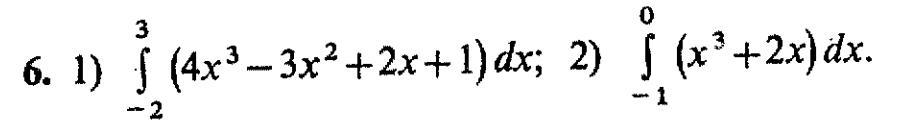
Ответы
Автор ответа:
1
Ответ:
Объяснение:
номер 4 делать аналогично 5, а = 1
kent2121:
а вторую картинку можешь?
Спасибо братан
Похожие вопросы
Предмет: Русский язык,
автор: enzheljve
Предмет: Українська мова,
автор: ksyha12345
Предмет: Русский язык,
автор: fyutkb
Предмет: Химия,
автор: KokonaHarukaStudent
Предмет: Математика,
автор: zhanseitovamari