Question

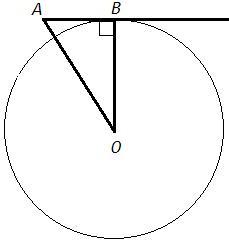
Из точки А к окружности с центром в точке О проведена касательная к данной окружности (точку касания обозначим через В). Найдите углы треугольника АОВ, если угол ВАО в 2 раза больше угла ВОА
ПОЖАЛУЙСТА ПОМОГИТЕ РЕШИТЬ​

Answer 1

Радиус (OB) в точку касания перпендикулярен касательной.

Треугольник AOB - прямоугольный.

Сумма острых углов прямоугольного треугольника 90.

O=x, A=2x

O+A=90 => 3x=90 => x=30

O=30, A=60