Предмет: Математика,
автор: JohnatanIve
Нужна помощь) Помогите решить этот чертов пример) Все никак не выходит)1 курс. Заранее благодарен.
Приложения:
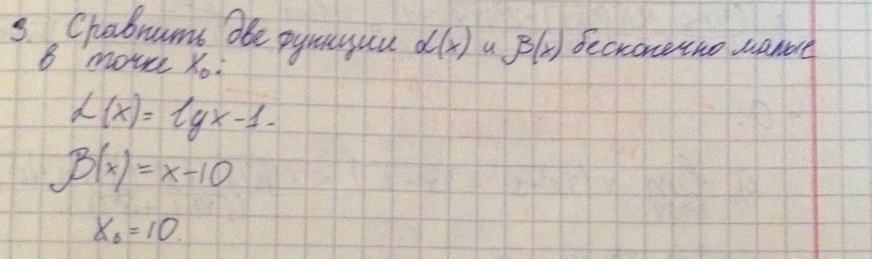
Ответы
Автор ответа:
0
Насчет второй функции более менее понятно. При  можно сделать замену: х-10=t, тогда получим, что
можно сделать замену: х-10=t, тогда получим, что  . Это бесконечно малая первого порядка.
. Это бесконечно малая первого порядка.
Намного сложнее с первой функцией.

по свойству логарифмов
Значит

При можно сделать замену:
можно сделать замену:  , тогда получим, что
, тогда получим, что  . Сама функция придет к виду
. Сама функция придет к виду

По другому, используя свойства логарифмов
 при
при  .
.
Заметим, что

Значит, что используя эквивалентности при

Значит бесконечно малая того же порядка, что и вторая функция (первого порядка), но при стремлении к нулю будет коэффициент равный
Ответ: первая функция является бесконечно малой первого порядка с коэффициентом при нуле равным ,
,
вторая функция является бесконечно малой тоже первого порядка с коэффициентом при нуле равным 1.
Намного сложнее с первой функцией.
по свойству логарифмов
Значит
При
По другому, используя свойства логарифмов
Заметим, что
Значит, что используя эквивалентности при
Значит бесконечно малая того же порядка, что и вторая функция (первого порядка), но при стремлении к нулю будет коэффициент равный
Ответ: первая функция является бесконечно малой первого порядка с коэффициентом при нуле равным
вторая функция является бесконечно малой тоже первого порядка с коэффициентом при нуле равным 1.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: elmuradrahimzanov210
Предмет: Қазақ тiлi,
автор: fmkfeliksFelix
Предмет: История,
автор: DianaDandy
Предмет: Математика,
автор: kalel