Question

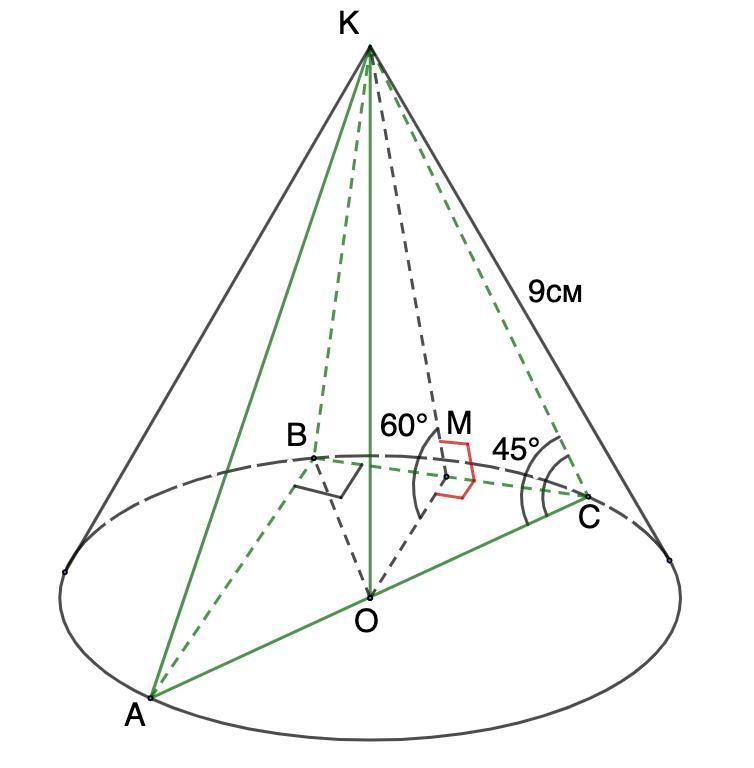
У конус вписано піраміду, основою якої є прямокутний трикутник. Бічна грань, що містить один з катетів основи, утворює з площиною основи кут 60°. Знайдіть об'єм піраміди (у см3), якщо твірна конуса дорівнює 9 см і нахилена до площини основи під кутом 45°.​

Answer 1

Ответ:

Объем пирамиды равен 81 см³.

Объяснение:

В конус вписана пирамида, основой которой является прямоугольный треугольник. Боковая грань, содержащая один из катетов основания, образует с плоскостью основания угол 60°. Найдите объем пирамиды (в см³), если образующая конуса равна 9 см и наклонена к плоскости основания под углом 45°.​

Дано: КАВС - пирамида, вписана в конус;

ΔАВС - прямоугольный - основание пирамиды;

∠КМО = 60°; ∠КСО = 45°;

КС = 9 см.

Найти: V(КАВС)

Решение:

Объем пирамиды:

$\displaystyle \bf \boxed { S=\frac{1}{3}SH }\;,$

где S - площадь основания, Н - высота пирамиды.

Прежде, чем решать задачу, определимся с чертежом.

Известно, что образующая конуса наклонена к плоскости основания под углом 45°.

⇒ каждое ребро пирамиды наклонены под тем же углом, так как она вписана в конус.

• Если в пирамиде все ребра наклонены под одним углом к основанию, то высота проектируется в центр описанной окружности.

• Центр описанной окружности около прямоугольного треугольника лежит на середине гипотенузы.

⇒ КО - высота пирамиды.

Далее проведем перпендикуляр из точки О к катету ВС, поставим точку М. М соединим с К.

• Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

⇒ КМ ⊥ ВС.

Значит ∠ОМК = 60° - угол наклона боковой грани к плоскости основания.

Теперь найдем высоту пирамиды КО.

1. Рассмотрим ΔОКС - прямоугольный.

∠КСО = 45° (условие)

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ОКС = 90° - 45° = 45°

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ ОС = ОК.

Пусть ОС = ОК = х, тогда по теореме Пифагора:

$\displaystyle \bf OC^2+OK^2=KC^2\\\\2x^2=81\\\\x=\frac{9}{\sqrt{2} } \\\\x=\frac{9\sqrt{2} }{2}$

⇒

$\displaystyle \bf OC=OK=\frac{9\sqrt{2} }{2}\;_{CM }$

Высоту нашли, теперь надо найти площадь основания, то есть ΔАВС.

• Площадь прямоугольного треугольника равна половине произведения катетов.

2. Рассмотрим ΔОКМ - прямоугольный.

$\displaystyle \bf OK=\frac{9\sqrt{2} }{2}\;_{CM };\;\;\;\;\;\angle{OMK}=60^0$ .

• Котангенс угла - отношение прилежащего катета к противолежащему.

$\displaystyle \bf \frac{OM}{OK}=ctg60^0\\ \\OM=\frac{9\sqrt{2} }{2}\cdot\frac{\sqrt{3} }{3}=\frac{3\sqrt{6} }{2}\;_{(CM)}$

3. Рассмотрим ΔОВС.

ОВ = ОС = R ⇒ ΔОВС - равнобедренный.

ОМ ⊥ ВС ⇒ ОМ - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ ВМ = МС

4. Рассмотрим ΔАВС - прямоугольный.

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ ОМ || АВ;

ВМ = МС;

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ ОМ - средняя линия ΔАВС.

• Средняя линия равна половине стороны, которую она не пересекает.

⇒ АВ = 2 ОМ;

$\displaystyle \bf AB=3\sqrt{6}\;_{CM};\\\\AC=2\;OC=9\sqrt{2}\;_{CM}$

По теореме Пифагора найдем ВС.

ВС² = АС² - АВ²

$\displaystyle \bf BC^2=81\cdot2-9\cdot6=108\\\\BC=6\sqrt{3} \;_{CM}$

$\displaystyle \bf S(ABC)=\frac{1}{2}\;AB\cdot{BC}=\frac{1}{2}\cdot3\sqrt{6}\cdot6\sqrt{3}=\\ \\ =9\cdot3\cdot\sqrt{2}=27\sqrt{2} \;_{(CM^2)}$

Объем пирамиды равен:

$\displaystyle \bf V(KABC)=\frac{1}{3}\cdot27\sqrt{2}\cdot\frac{9\sqrt{2} }{2} =81\;_{(CM^3)}$

#SPJ5