Предмет: Геометрия,
автор: Аноним
Помогите
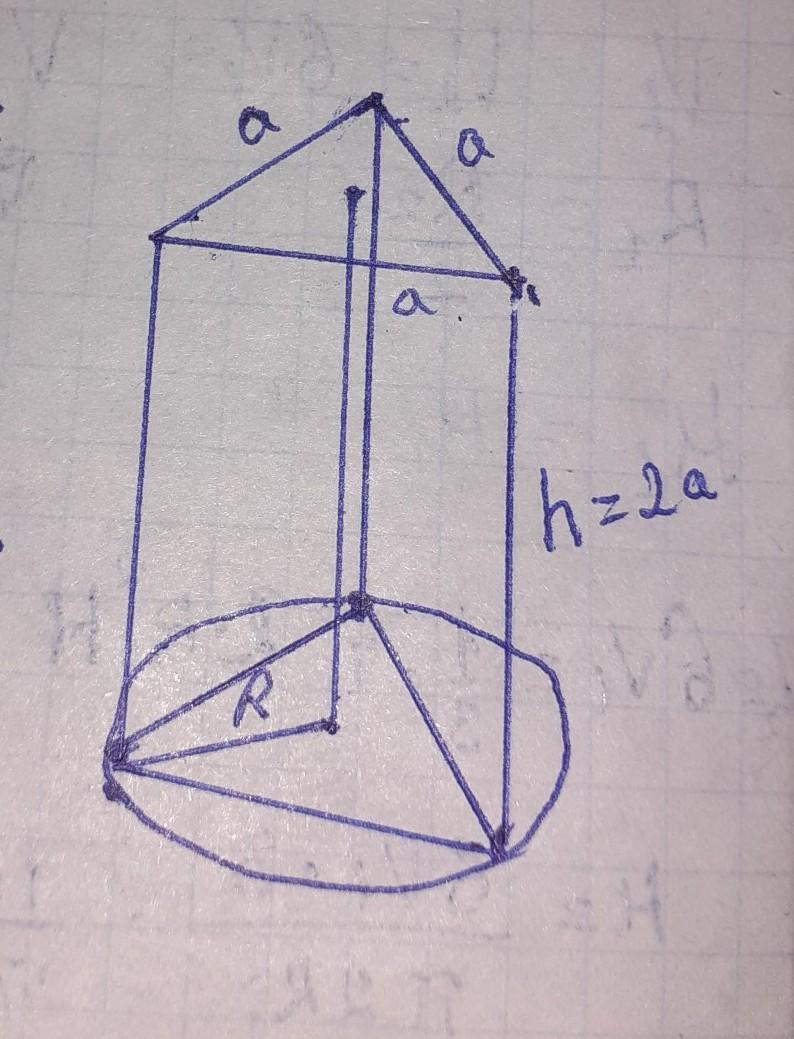
Радиус окружности, описанной вокруг основания правильной треугольной призмы равна 3√3 см. Найти площадь ее боковой поверхности, если ее высота вдвое больше, чем сторона основания.
Ответы
Автор ответа:
0
R=3√3 см
Н=2а
Sб.п - ?
на основании правильной треугольной призмы лежит равносторонний треугольник
радиус описанной около равностороннего треугольника
R=a/√3 отсюда сторона треугольника
а=R×√3=3√3 ×√3=9 см
высота Н=2а=2×9=18 см
площадь боковой поверхности призмы
Sб.п=Р×Н=3а×Н=3×9×18= 486 см²
здесь P=3a периметр основания
Приложения:
Аноним:
А тут 3√3*3=9√3
А всё правильно извините
Похожие вопросы
Предмет: Русский язык,
автор: sophya1205
Предмет: Русский язык,
автор: AXEES
Предмет: Английский язык,
автор: Ольчик83
Предмет: Математика,
автор: VKUNIKHINA
Предмет: Математика,
автор: knowledge228