Предмет: Математика,
автор: JohnatanIve
Привет! Помогите решить это плиз, целый час уже бьюсь над этим заданием.
Нужно вычислить производную по правилам и формулам дифференцирования
Приложения:
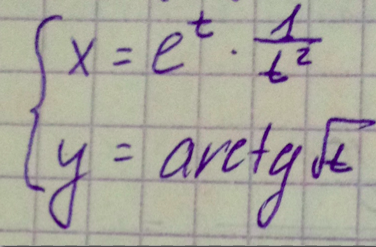
Ответы
Автор ответа:
0
Я так понимаю, первую производную.
Есть такая формула

Теперь найдем


Теперь найдем отношение



Ответ:
Есть такая формула
Теперь найдем
Теперь найдем отношение
Ответ:
Похожие вопросы
Предмет: Биология,
автор: vfilipcov
Предмет: Информатика,
автор: yudinnikitos2017
Предмет: Қазақ тiлi,
автор: zanarkosalieva5
Предмет: Математика,
автор: Valad
Предмет: Биология,
автор: Аноним