Предмет: Геометрия,
автор: Mad7Max
Решите с чертежом пожалуйста
Приложения:

Ответы
Автор ответа:
1
Доказательство:
∆АОВ имеет с ∆СОВ одну общую сторону ВО, равные углы АВО и СВО (биссектриса), равные углы АОВ и СОВ. Значит, треугольники равны по стороне и двум прилежащим к ней углам. Следовательно, угол ВАО = углу ВСО (т.к. в равных треугольниках соответственные углы равны).
Если АО и СО - биссектрисы, то и углы ОАС с ОСА равны. Значит, треугольник АВС равнобедренный, основание - АС.
Решение:
Если полные угол О = 360°, то угол АОС = 360 - 110 - 110 = 150°. Следовательно, углы ОАС и АСО по: (180-150):2=15°. Если АО и СО - биссектрисы, то каждый из углов ВАС и ВСА по 15+15=30°. По сумме углов треугольника АВС ищем угол В. Угол В = 180-(30+30)=120°.
Ответ: угол В = 120°, углы А и С по 30°.
Приложения:
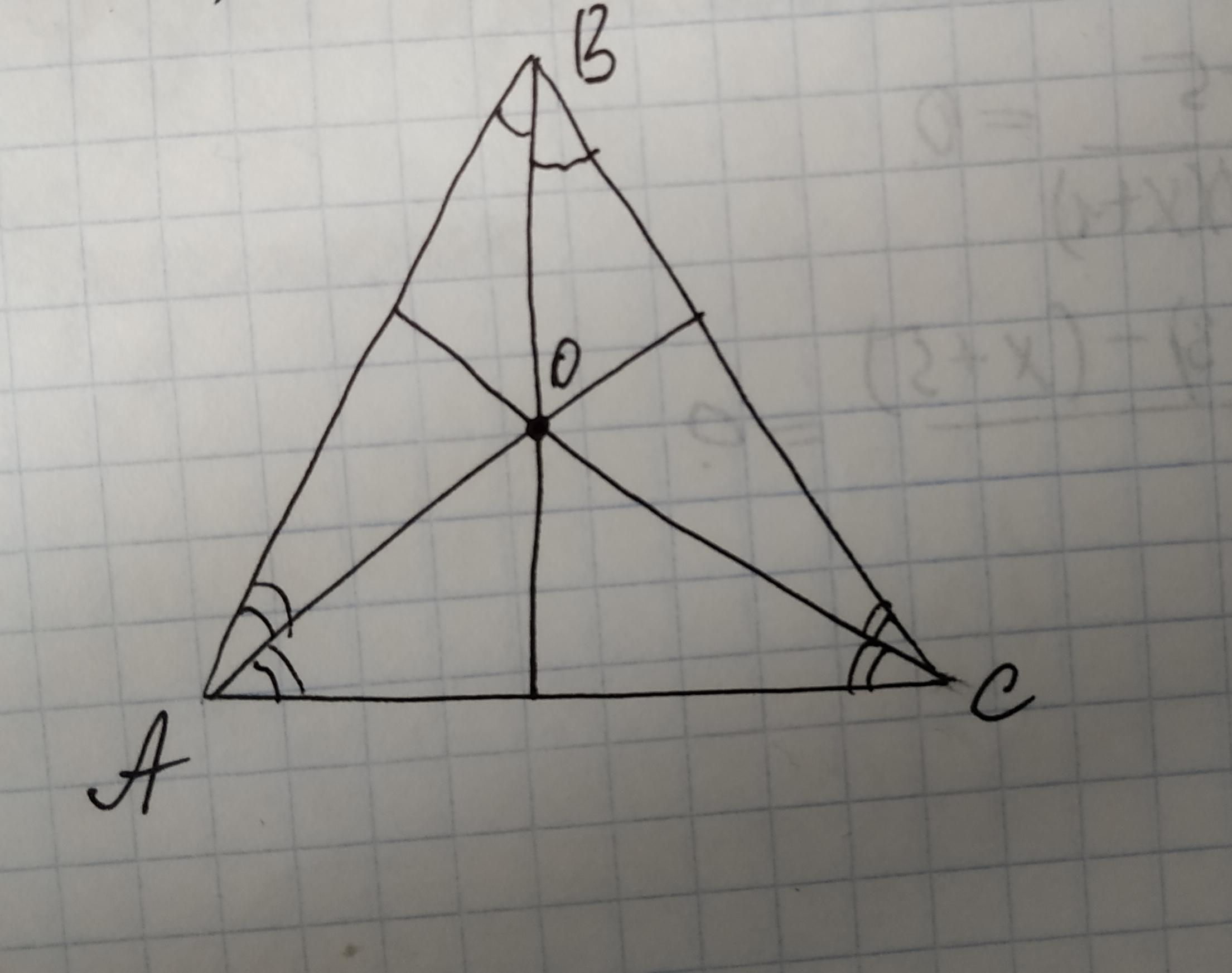
Похожие вопросы
Предмет: Русский язык,
автор: ALOPPA
Предмет: Русский язык,
автор: leraagapowa
Предмет: Русский язык,
автор: serbu
Предмет: Геометрия,
автор: HastushAnd
Предмет: Физика,
автор: Eliza1111115