Упростить выражение. Помогите пожалуйста. Желательно с объяснением)




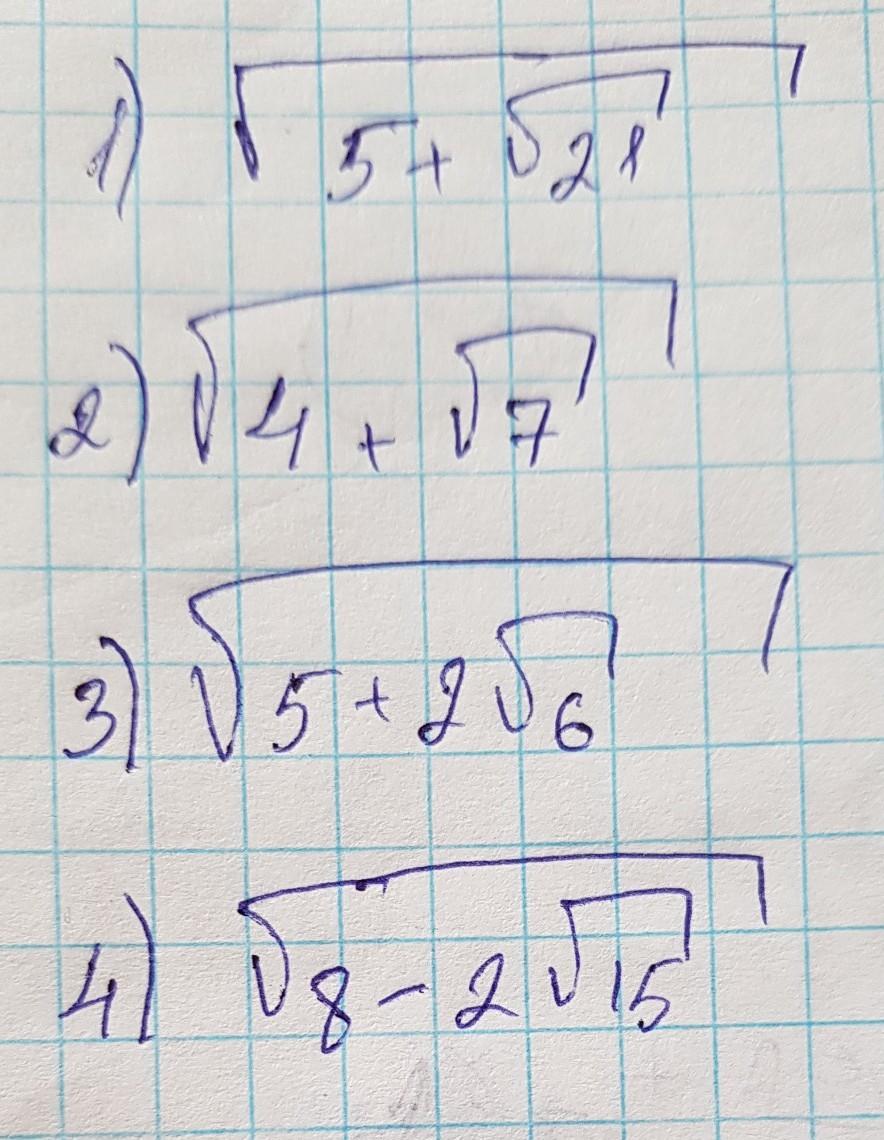
Ответы
Ответ:
√(5+√21)=1/2(√14+√6)
Остальные точно такие же. В последнем представить, как квадрат разности. Порешай по этому образцу.
Объяснение:
√(5+√21);
Необходимо избавиться от внешнего радикала. Для этого представить выражение под радикалом в виде квадрата суммы:
√(a²+2ab+b²)=√(a+b)²=l a+b l (по модулю, потому что под квадратным корнем выражение должно быть положительным.
Вот и превратим рациональное число в сумму квадратов, а иррвциональное - в удвоенное произведение:
a²+b²=5;
2ab=√21;
Решаем:
2ab=√21
b=√21/(2a);
а≠0
Подставляем:
a²+(√21/2a)²=5;
a²+21/4a²=5
Биквадратное:
4a⁴+21=5*4a²;
4a⁴-20a²+21=0;
делаем замену:
a²=z
4z²-20z+21=0;
D=400-336=64
z₁₂=1/8(20±8);
z₁=28/8=7/2; z₂=12/8=3/2;
a²=z
a²₁₂=7/2; a₁₂=±√(7/2)
a²₃₄=3/2; a₃₄=±√(3/2);
Всего четыре корня. Берем, например, первый
b=√21/2a;
b=√21/(2√(7/2))=√(21*2)/√28=√(3*7*2)/4*7)=√(3/2);
Проверка:
√(√(7/2))²+2√(7/2)√(3/2)+(√(3/2)²)=
7/2+2√(21/4)+3/2=5+√21; Правильно!
Продолжаем:
√(√(7/2))²+2√(7/2)√(3/2)+(√(3/2)²)=√(√(7/2)+√(3/2))²=
l√(7/2)+√(3/2)l=√(7/2)+√(3/2)=1/(√2)(√7+√3)=1/2((√2)(√7+√3))=1/2(√14+√6)