Предмет: Алгебра,
автор: Schofy88
N 609. ПОМОГИТЕ РЕШИТЬ.
Система неравенств
Приложения:
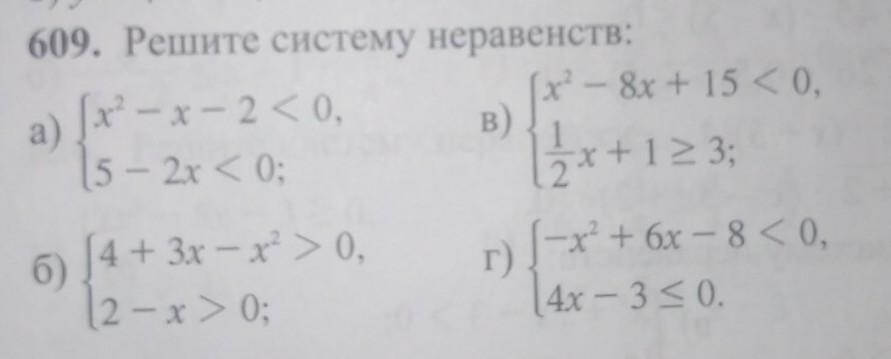
Ответы
Автор ответа:
8
Schofy88:
Огромное спасибо, что помогаешь людям. Как появится возможность, отмечу твой ответ как лучший
Похожие вопросы
Предмет: Русский язык,
автор: zvey
Предмет: Русский язык,
автор: 1санта1
Предмет: Русский язык,
автор: СЕРГЕЙПО
Предмет: Информатика,
автор: OlgaBoyko