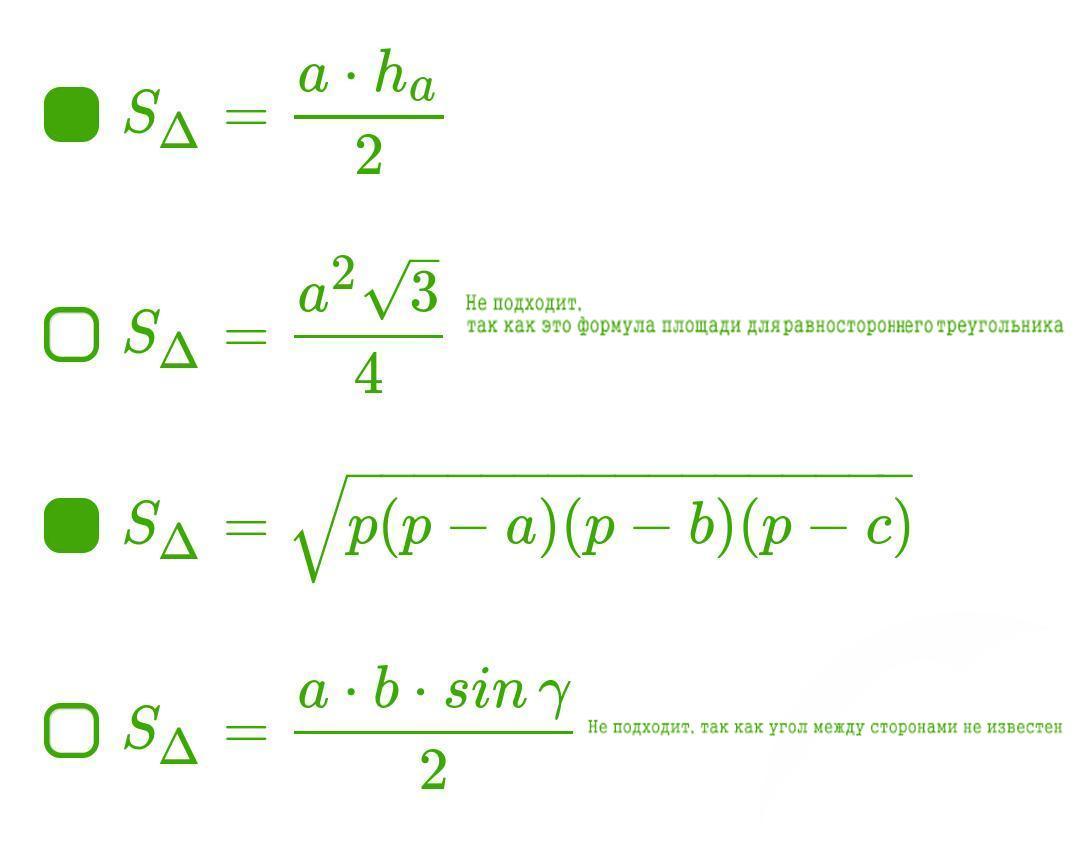Question

Срочно помогите пожалуйста
Только можете тот кто шарит в геометрии, в интернете ответы не верны
Стороны треугольника равны 17 дм, 21 дм, 10 дм.
Вычисли наибольшую высоту этого треугольника.

Наибольшая высота равна
дм

Answer 1

Ответ:

Будем решать методом площадей.

S=√(p(p-a)(p-b)(p-c), где а, b,c - стороны треугольника, р- полупериметр

S=0,5*h*a, где а-сторона, h-высота. Наибольшая высота будет проведена к наименьшей стороне, то есть а=10дм.

р(р-а)(р-в)(р-с)=0,25*h²*10²

p=(17+21+10)/2=24

24(24-17)(24-21)(24-10)=25h²

24*7*3*14=25h²

h²=24*7*3*14/25

h=√(3*4*2*7*3*7*2/25)= √(3²*2²*2²*7²/5²)=3*2*2*7/5=12*7/5=84/5=168/10=16.8(дм)

Ответ: 16,8 дм.

Answer 2

В треугольнике наибольшая высота - высота, проведённая к наименьшей стороне треугольника.

В данном случае наименьшая сторона равна 10 дм.

Найдём площадь по формуле Герона.

Полупериметр равен $\frac{17+21+10}{2} =24$ дм.

$S=\sqrt{24(24-10)(24-17)(24-21)} =\sqrt{7056} =84$ дм^2.

S = наибольшая высота*наименьшая сторона*0,5

84 = 5*наибольшая высота

Наибольшая высота = 16,8 дм.

Формулы для решения этой задачи прикрепила в картинке.

Площадь треугольника равна 84 дм^2.