Предмет: Геометрия,
автор: pliscro4no
Катети прямокутного трикутника дорівнюють 30 см та 40 см.
Обчисли радіус описаного кола та радіус вписаного кола.
Відповідь:
R= [ ]см; r= [ ]см;
Ответы
Автор ответа:
2
Радіус кола, вписаного в прямокутний трикутник, знаходиться за формулою:
r = (a + b - c) / 2,
де a і b - катети, c - гіпотенуза.
За умовою a = 30 см, b = 40 см.
По теоремі Піфагора знайдемо гипотенузу з:
c ^ 2 = a ^ 2 + b ^ 2;
з = √ (a ^ 2 + b ^ 2);
з = √ (30 ^ 2 + 40 ^ 2) = √ (900 + 1600) = √2500 = 50 (см).
Підставами відомі значення в формулу радіуса вписаного кола і знайдемо довжину радіуса:
r = (30 + 40 - 50) / 2 = 20/2 = 10 (см).
Відповідь: r = 10 см.
2) радіус Описаної окружності = фото
Ответ : R=25
r = (a + b - c) / 2,
де a і b - катети, c - гіпотенуза.
За умовою a = 30 см, b = 40 см.
По теоремі Піфагора знайдемо гипотенузу з:
c ^ 2 = a ^ 2 + b ^ 2;
з = √ (a ^ 2 + b ^ 2);
з = √ (30 ^ 2 + 40 ^ 2) = √ (900 + 1600) = √2500 = 50 (см).
Підставами відомі значення в формулу радіуса вписаного кола і знайдемо довжину радіуса:
r = (30 + 40 - 50) / 2 = 20/2 = 10 (см).
Відповідь: r = 10 см.
2) радіус Описаної окружності = фото
Ответ : R=25
Приложения:
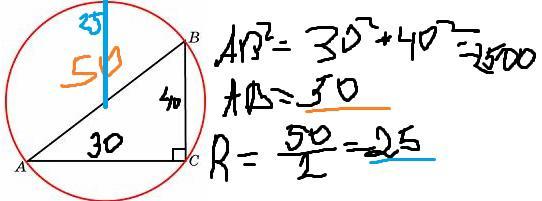
Похожие вопросы
Предмет: Русский язык,
автор: anyastroganova1
Предмет: Английский язык,
автор: нимак
Предмет: Русский язык,
автор: bulanina03
Предмет: Обществознание,
автор: oleg569
Предмет: Математика,
автор: 55555269