Question

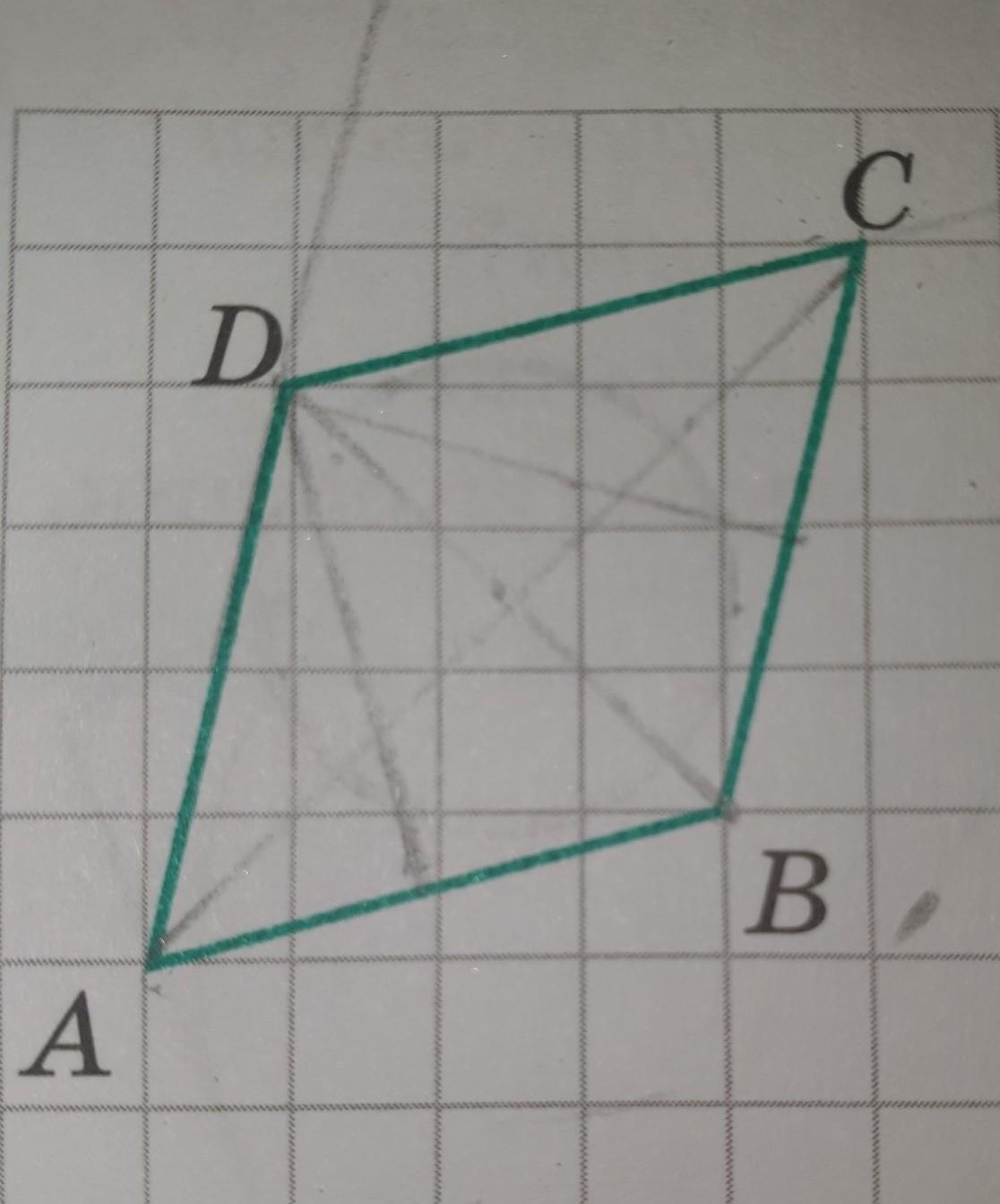
найдите радиус окружности , вписанной в ромб, изображенный на рисунке . ​

Answer 1

Ответ:

$r = \frac{7.5}{ \sqrt{17}}$

Объяснение:

1. прямоугольный треугольник с катетами =5, => гипотенуза АС=5√2

2. прямоугольный треугольник с катетами =3, => гипотенуза BD=3√2

3. площадь ромба равна полу произведению диагоналей:

$s = \frac{5 \sqrt{2} \times 3 \sqrt{2}}{2} = 15$

4. площадь ромба равна произведению стороны на высоту

s=a×h

сторона ромба а:

${a}^{2} = {4}^{2} +{1}^{2} \\ {a}^{2} = 17 \\ a = \sqrt{17}$

15=√17×h

$h = \frac{15}{ \sqrt{17} }$

h=d - диаметру окружности вписанной в ромб

h=2r

$r = \frac{15}{ \sqrt{17} } \div 2 = \frac{7.5}{ \sqrt{17} }$