Question

Пожалуйста помогите !!!
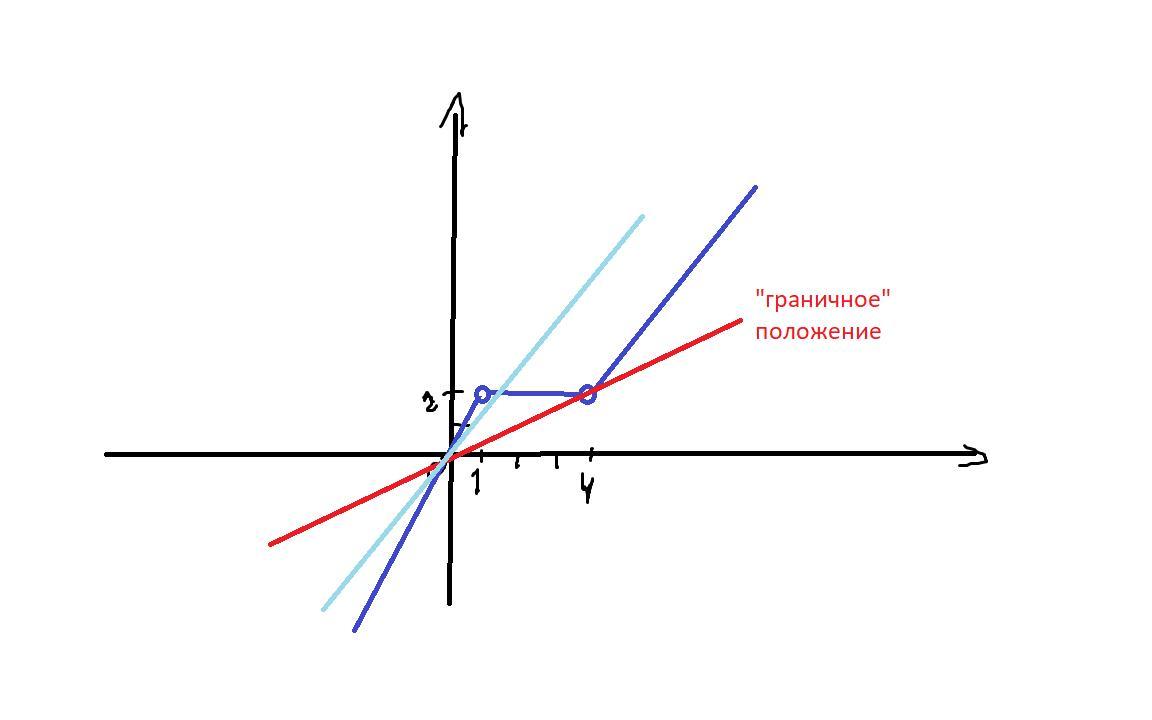
Дана функция y = f (x), где f (x) = {2x, если x<1
{2, если 1< x < 4
{ 2 x - 6 , если x > 4 Найдите, при каких значениях k уравнение f (x) = kx имеет три корня.

Answer 1

Ответ:

(2; 0,5)

Пошаговое объяснение:

Очевидно, К=2 нам не подходит, т.к. такая прямая (F(x) = kx - линейная функция, график прямая) будет совпадать с 2х.

Рассмотрим график; чтобы было три пересечения, прямая должна пересекать все три "куска" графика.

1. Первую часть, у=2х, пересекает при К!=2.
2. Вторую часть, у=2, пересекает при всех К принадлежащих интервалу (2;0.5) - 0.5 получаем из уравнения 2=4К (берем "граничное" положение (при котором УЖЕ нельзя найти три пересечения) F(x)=kx и подставляем.
3. Третью часть пересекает при соблюдении первого условия, т.к. если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую.

Имеем К!=2 и 2<K<0,5 => К принадлежит (2; 0,5).