Предмет: Математика,
автор: drobott99
Помогите пожалуйста с высшей математикой!
Приложения:
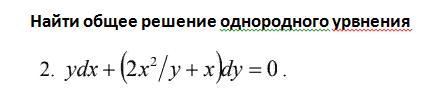
Ответы
Автор ответа:
2
Проверим особые решения
Верно.
Неверно, а значит y=-2x не является решением.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: довженко00
Предмет: Русский язык,
автор: 0lenka
Предмет: Русский язык,
автор: АААнгелина
Предмет: Математика,
автор: полина1495