Предмет: Геометрия,
автор: David240204
Один из углов треугольника равен 30° ,а противолежащая ему сторона равна 4,8 дм. Найдите радиус описанной около этого треугольника окружности.
СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
siestarjoki:
Теорема синусов: 4,8/sin30 =2R => R=4,8
Другое решение. Угол 30 и центральный угол описанной окружности опираются на одну дугу. Центральный угол 60, два радиуса и сторона образуют равносторонний треугольник, радиус равен стороне.
Ответы
Автор ответа:
102
Ответ:
4,8 дм
Объяснение:
Приложения:
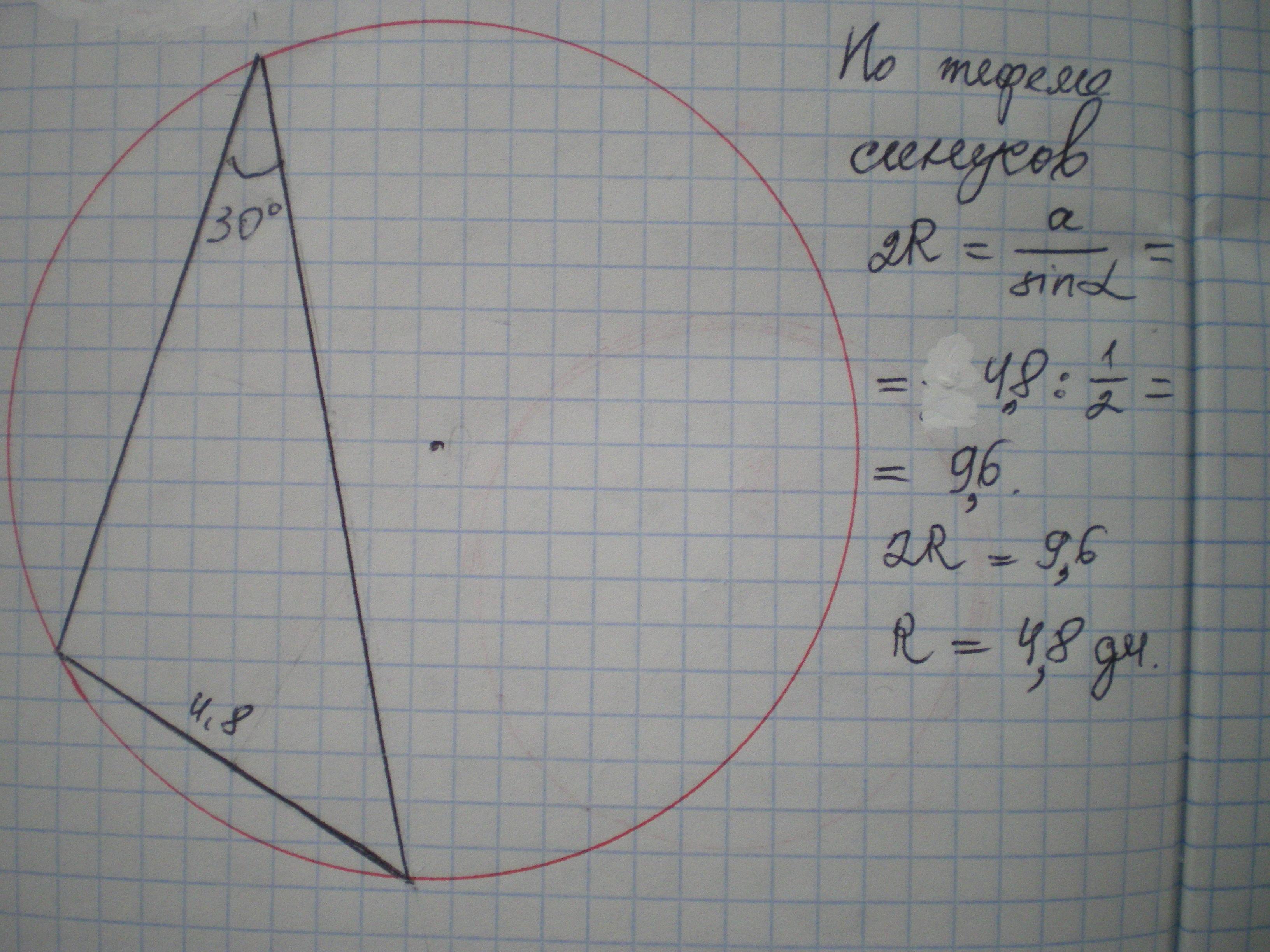
Автор ответа:
56
Ответ:
R = 4,8 дм.
Объяснение:
1. По теореме синусов , где
- 4,8 дм,
. Вставим в формулу известные величины и вычислим радиус.
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: Bronskiy
Предмет: Русский язык,
автор: Loveлось
Предмет: Русский язык,
автор: ПавелPavel
Предмет: История,
автор: dasha9753
Предмет: Алгебра,
автор: nazaresha80