Предмет: Геометрия,
автор: smeshok324
ПОМОГИТЕ ПОЖАЛУЙСТА. РЕШИТЕ ПОДРОБНО
В равнобедренном треугольнике KLC проведена биссектриса CM угла C у основания KC,
∡ CML = 78°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
∡ K =
°;
∡ C =
°;
∡ L =
°.
Приложения:

Ответы
Автор ответа:
5
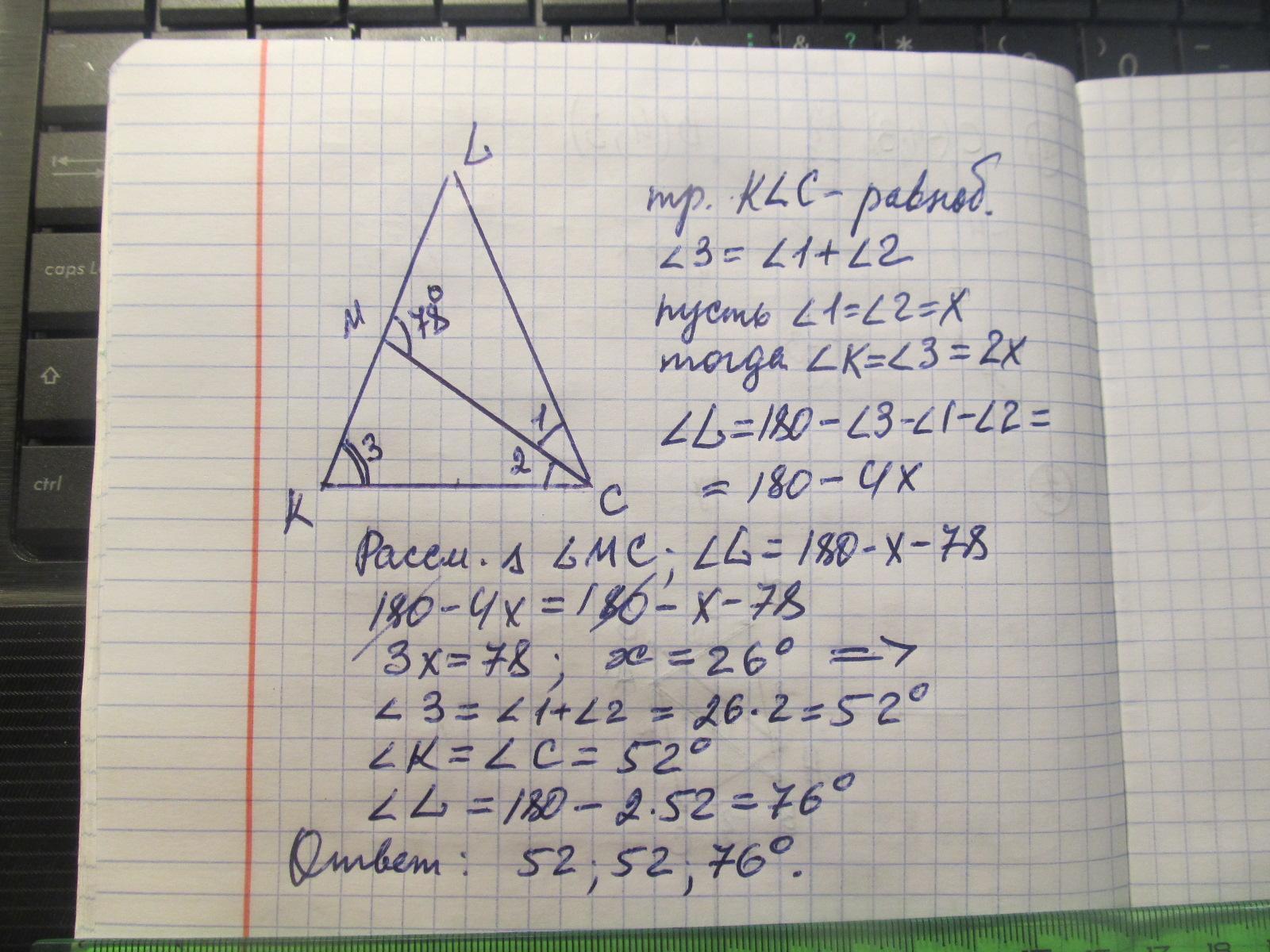
Решение на фото/////
Приложения:
Автор ответа:
0
Ответ: угол L=76°; угол С= углу К=52°
Объяснение: Биссектриса СМ делит ∆KLC на два других треугольника. Рассмотрим полученный треугольники СМК и LMC. По условиям угол CML=78°, тогда, угол СМК в ∆СКМ=180-78=102°;
Угол СМК=102°
Зная, что ∆KLC- равнобедренный, то угол К=углу С. Так как биссектриса СМ делит угол С пополам, угол КСМ в ∆СКМ буде в 2 раза меньше угла К. Пусть угол КСМ=х, тогда угол К=2х. Так сумма всех углов треугольника равна 180°, Составляем уравнение:
х+2х+102=180
3х+102=180
3х=180-102
3х=78
х=26
Часть угла, полученного при делении биссектрисой=26°
Найдём угол К: угол К=26×2=52;
угол К=52°; теперь найдём угол L:
180-52×2= 180-104=76; угол L=76°
Похожие вопросы
Предмет: Русский язык,
автор: murugova71
Предмет: Русский язык,
автор: virus9911
Предмет: Русский язык,
автор: nuka24
Предмет: Математика,
автор: AlinaTsurskaya9
Предмет: Математика,
автор: lusia888