Предмет: Алгебра,
автор: swetlanaprya
Помогите решить уравнение (номер 845)
Приложения:

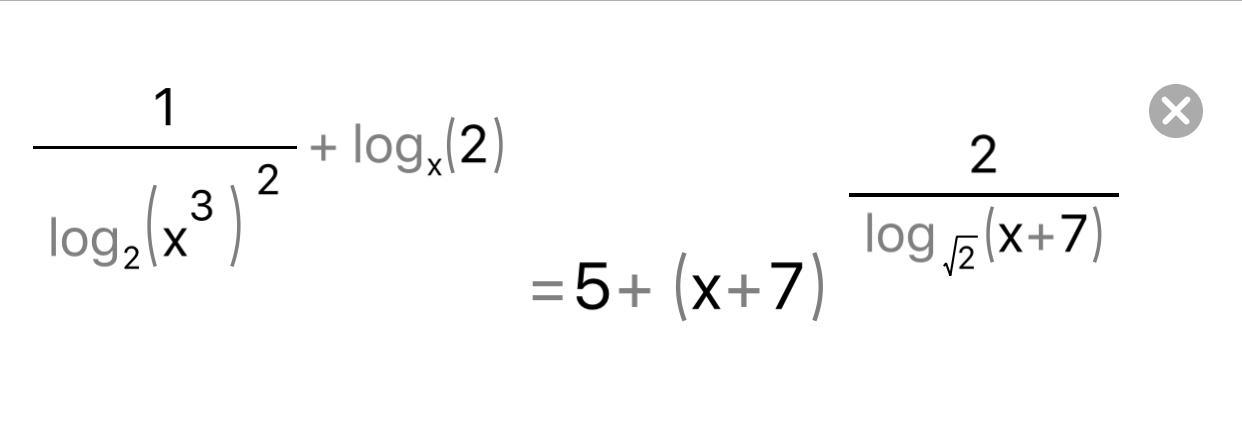
aastap7775:
оснований не видно(
Прикрепила ещё одну фотографию
там де еще 7 слева
Даа, просто я ввела, но весь пример на экран не вместился
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: 130584
Предмет: Английский язык,
автор: dashaosina
Предмет: Английский язык,
автор: мальда
Предмет: Математика,
автор: Аноним
Предмет: Музыка,
автор: WallkerYT