«Решение показательных и логарифмических уравнений»
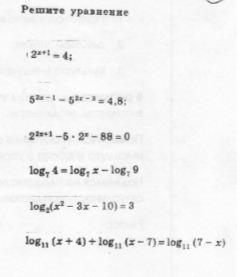
Ответы
1) 2^(x+1)=4
2^(x+1)=2^2
x+1=2
x=2-1
x=1
2) 5^(2x-1)-5^(2x-3)=4,8
5^(2x-3)*(5^2+1)=4.8
5^(2x-3)*26=4.8
5^(2x-3)=4.8/26
2x=log5(4.8/26)
x=log5(4.8/26)
3) 2^(2x+1)-5*2^x-88=0
2^(2x+1)-5*2^x=88
2^(2x)*2-5*2^x-88=0
Вводим новую переменную:
2^x=t
2t^2-5t-88=0
{t1=-5.5} {t2=8}
Подставляем:
2^x=t.
2^x=-5.5 2^x=8
x=log2(-5.5). 2^x=2^3
x1 не подходит x2=3
Ответ: x=3
4) log7(4)=log7(x)-log7(9)
log7(4)=log7(x/9)
log7(4)-log7(x/9)=0
x/9=7^(log7(4))
x=36
5) log2(x^2-3x-10)=3
log2(x^2-3x-10)=log2(8)
x^2-3x-10=8
x^2-3x-18=0
x1=6
x2=-3
Подставляем X для проверки
x=6
log2(6^2-3×6-10)=3
Подходит
x=-3
log2(3^2-3×3-10)=3
log2(-10)=3
Не подходит
Ответ: x=6
6) log11(x+4)+log11(x-7)=log11(7-x)
(x+4)(x-7)=(7-x)
x^2-3x-28=7-x
x^2-2x-35=0
x1= -5,. x2=7
x1 не подходит
Х2 подходит
Ответ: x=7