Предмет: Алгебра,
автор: swetlanaprya
Помогите решить логарифмическое уравнение (тут очень странно написано, это немного смущает)
Приложения:
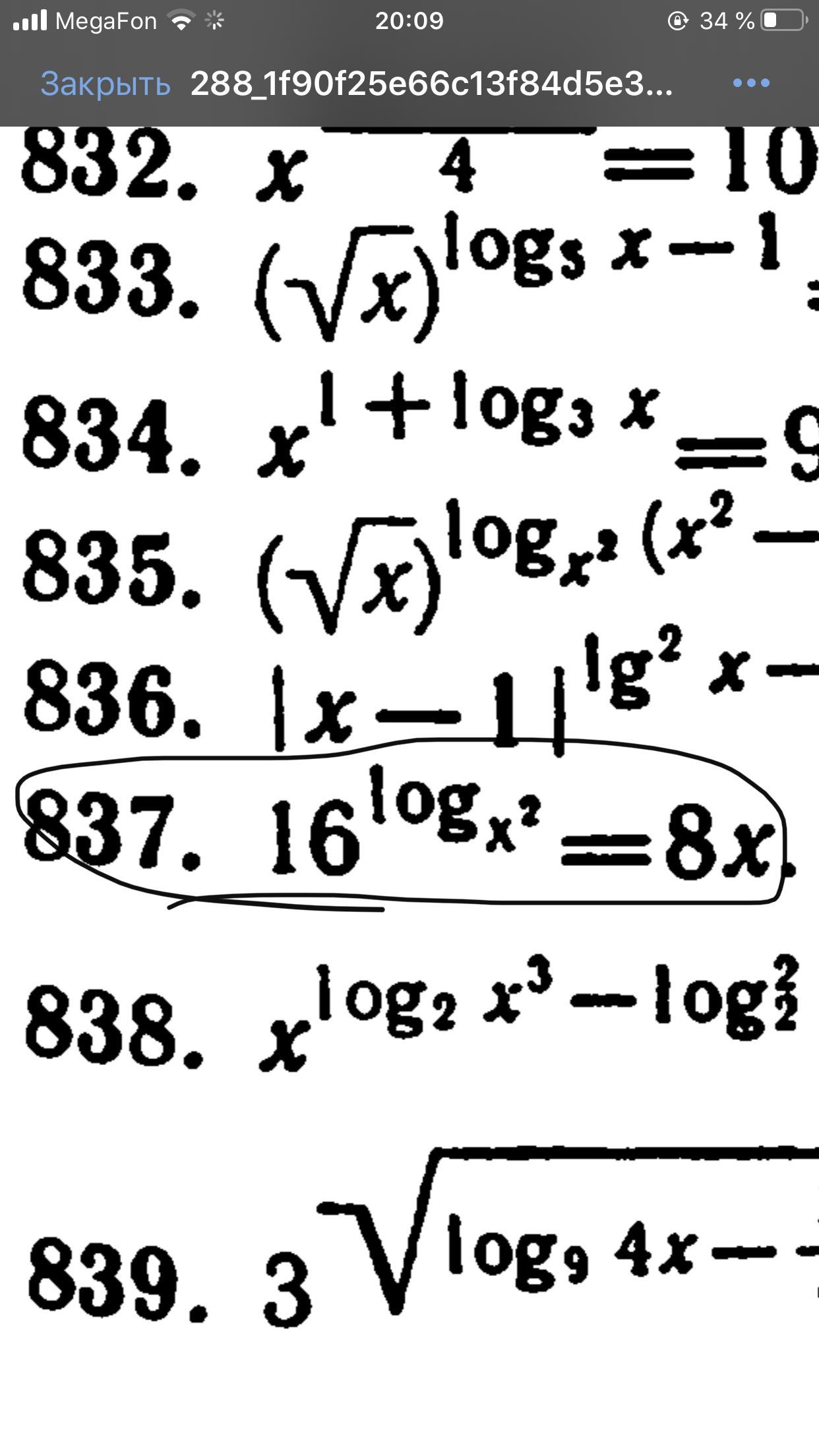
aastap7775:
опечатка.
Я думаю, что здесь log 2 по основанию х
а ответ есть?
Да, 1/16 и 2
если ответ такой, то да: logx2
все верно записано и решаемо
прологарифмируйте обе части по основанию 2 для начала...
Окей, спасибо всем за помощь)
Ответы
Автор ответа:
2
Ответ:
1/16; 2
Объяснение:
ОДЗ: x>0, x≠1
Прологарифмируем по основанию 2
Спасибо, но я уже разобралась
Похожие вопросы
Предмет: Русский язык,
автор: Sysnova
Предмет: Русский язык,
автор: katyunchik2
Предмет: Русский язык,
автор: ftfgcfgh
Предмет: Математика,
автор: anna2241
Предмет: Литература,
автор: Arsenrubenia