Question

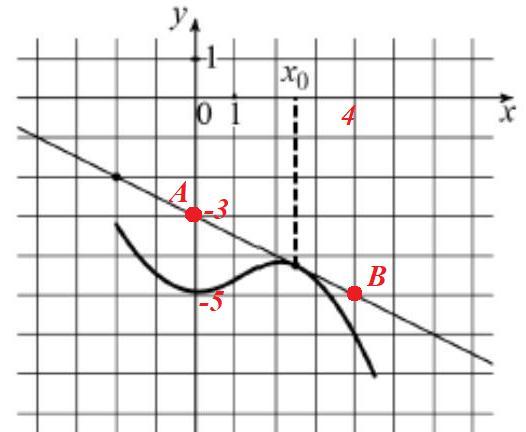
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.​

Answer 1

Значение производной функции в точке x₀ равно угловому коэффициенту касательной в этой точке.

Выбираем на касательной две любые точки, например:

A(0; -3)  и  B(4; -5).

Уравнение касательной  $y=kx+b$.

Подставляем координаты точки А:

$-3=k\cdot 0+b;\ \ \ \ b=-3$

Тогда уравнение касательной имеет вид:

$y=kx-3$

Подставляем координаты точки В:

$-5=k\cdot 4-3;\ \ \ 4k=-2;\ \ \ \boldsymbol{k=-0,5}$

$f'(x_0)=k=-0,5$

Ответ: $\boldsymbol{f'(x_0)=-0,5}$