Предмет: Математика,
автор: kinvanlunhalida
помогите пожалуйста помогите я не могу уже нечего делать!!!!!!!!
Приложения:
Ответы
Автор ответа:
1
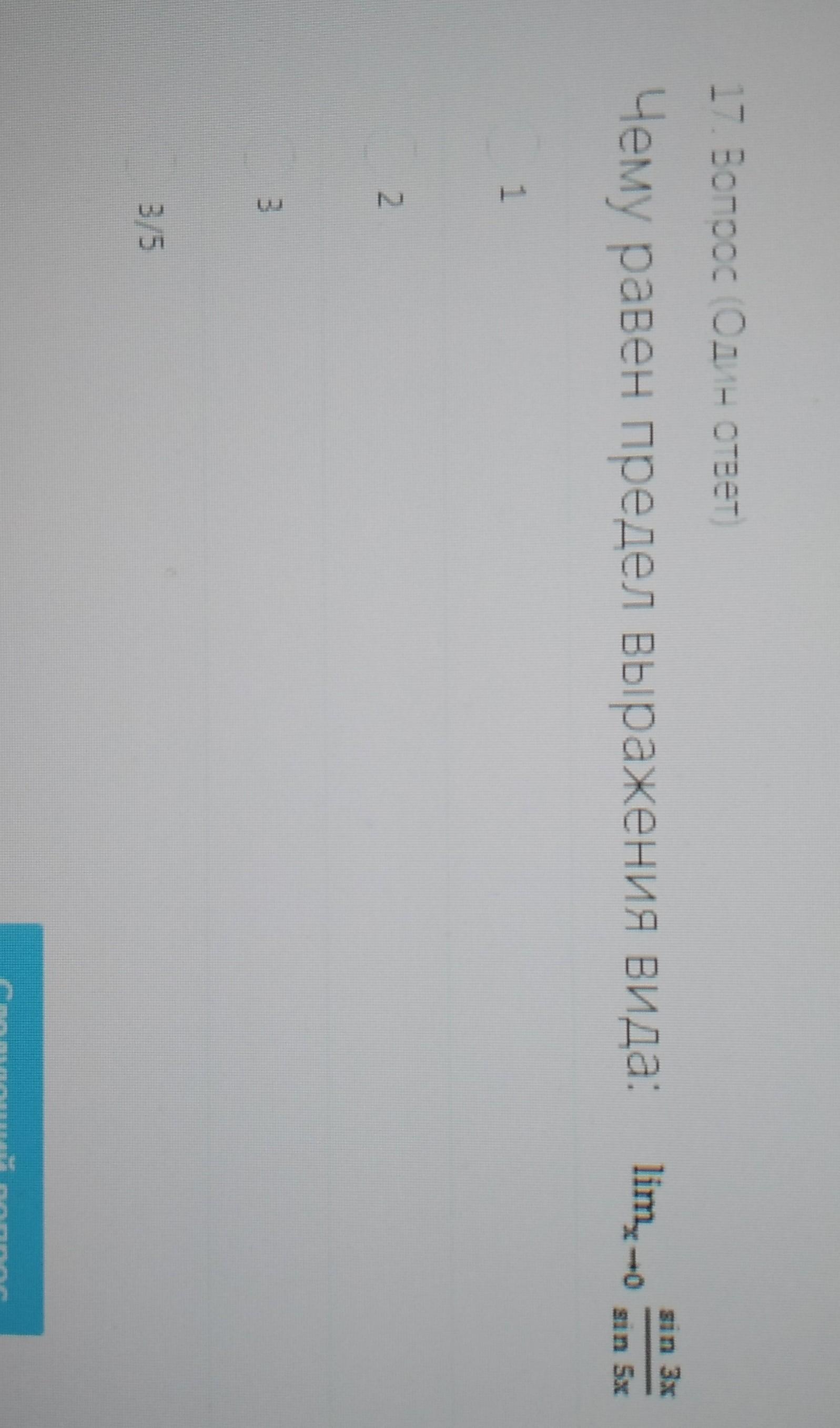
Ответ: 3/5.
Пошаговое объяснение:
Неопределённость 0/0. ⇒
Берём одновременно производную от числителя и знаменателя:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Українська мова,
автор: алинкакотикова
Предмет: Английский язык,
автор: v10945301
Предмет: Математика,
автор: Nawa111
Предмет: Математика,
автор: Аноним