Question

Волк и семеро козлят встали в один ряд и играют в чехарду: каждую секунду двое из них, стоящие через одного, могут, прыгнув, поменяться местами. Если окажется, что они стоят в обратном порядке по сравнению с исходным, игра заканчивается. Закончится ли игра?

Answer 1

Ответ:

Пошаговое объяснение:

Нет

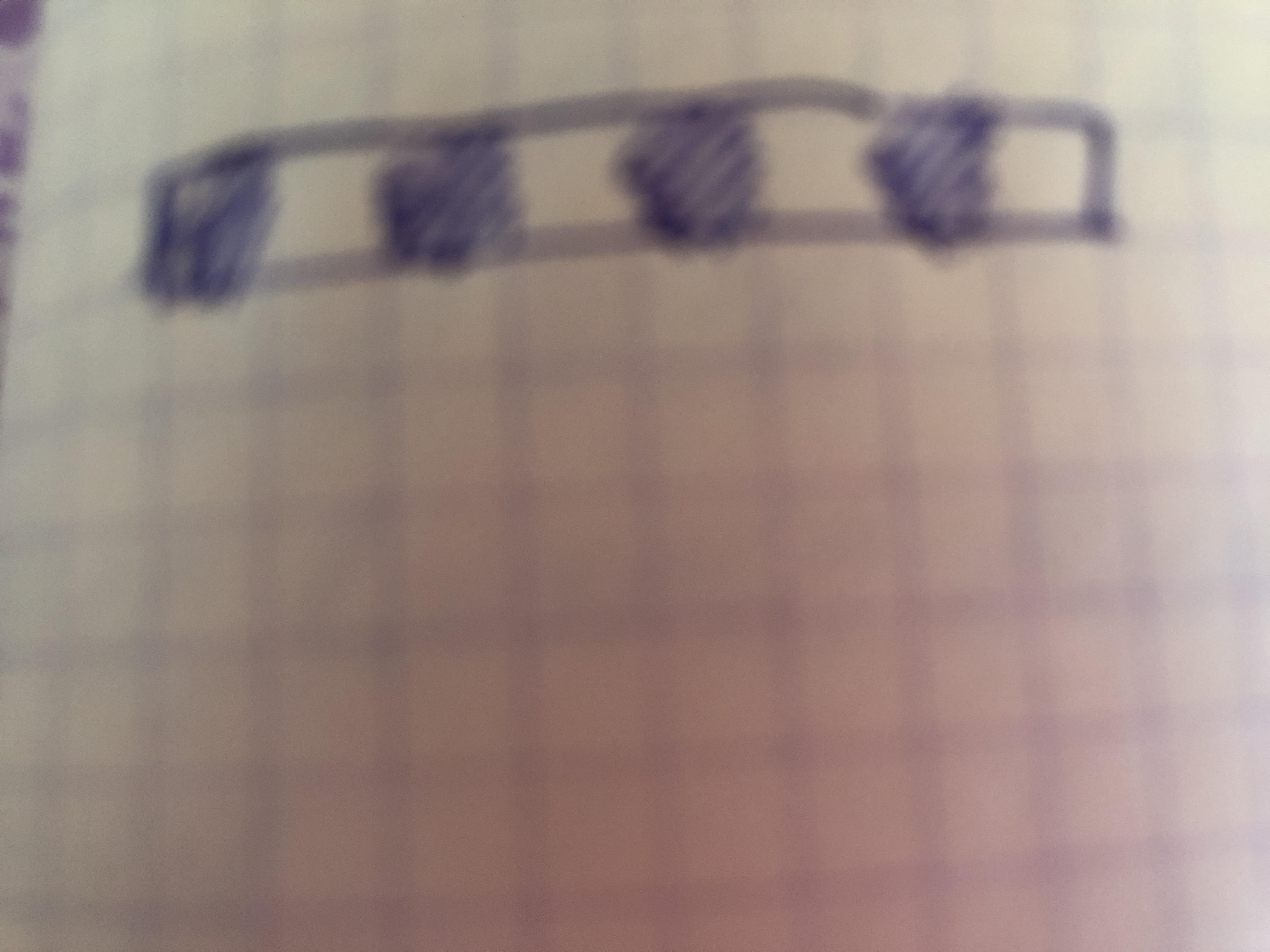
Чтобы понять можно использовать раскраску(я не знаю, знаешь ли ты что это такое но попробую объяснить), вообщем раскраска это специально придуманный способ доказательства каких нибудь математических вещей, где нужна какая то определенная привязка к местам(полезная короче вещь). Вообщем тут применим обычную шахматную раскраску, или, скажем так, через одну клеточку(см фото).

Те, кто стоят на чёрных клеточках могут попасть только на чёрные, а те кто на белых-на белые. Из рисунка очевидно, что крайний никак не доберётся до другой крайней, так как она всегда противоположного цвета.

То есть таким образом, ответ в четности, если бы было нечетное количество участников, все было бы круто.