Предмет: Математика,
автор: end39
Можете помочь мне решить этот неопределенный интеграл?
Приложения:
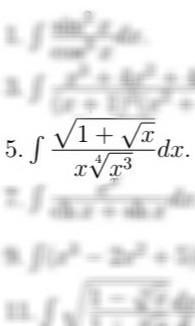
Ответы
Автор ответа:
1
Alexandr130398:
минус потеряли
Да, точно, спасибо.
А Вы в какой программе пишете?
геогебра
понял, спасибо)
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: Whispers
Предмет: Другие предметы,
автор: sovyniya
Предмет: Русский язык,
автор: zvereffvitalik
Предмет: Геометрия,
автор: 54т645пр