Предмет: Геометрия,
автор: Kolyayt
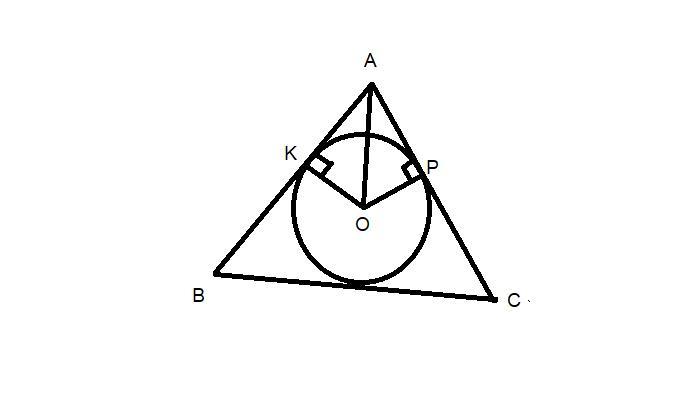
В треугольник АВС вписана окружность с центром О. Из точки О к сторонам АВ и АС треугольника проведены перпендикуляры ОК и ОР. Докажите, что АК=АР.
Ответы
Автор ответа:
2
Прямоугольные треугольники равны по гипотенузе и катету
OK=OP=R
OA-общая, значит равная
AK⊥OK и AP⊥OP так как касательные перпендикулярны радиусу вписанной окружности
Из равенства треугольников следует равенство соответствующих катетов AK=AP в этих треугольниках
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: alekspav1983
Предмет: Русский язык,
автор: Alekseika5204
Предмет: Русский язык,
автор: Varina22
Предмет: Алгебра,
автор: nqawdyhyh
Предмет: Математика,
автор: paliieva