Предмет: Геометрия,
автор: harlanmax
Докажите что треугольник MPK= треугольнику PMN, если известно, что 1)MK = PN 2)угол KMP = углу NPM
СРОЧНО, ПОЖАЛУЙСТА, 89 БАЛЛОВ
Приложения:
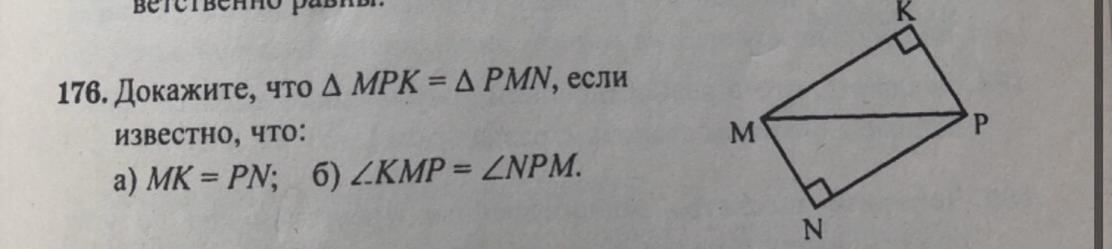
Ответы
Автор ответа:
6
ΔMPK = ΔPMN по первому признаку равенства треугольников — по двум сторонам и углу между ними:
MK = PN — по условию;
MP — общая сторона;
∠KMP = ∠NPM — по условию.
Дополнительно, т.к. треугольники ΔMPK и ΔPMN — прямоугольные (∠MKP = PNM) они равны по следующим признакам:
- по катету и гипотенузе: катет MK = PN — по условию, гипотенуза MP — общая;
- по гипотенузе и острому углу: гипотенуза MP — общая, ∠KMP = ∠NPM — по условию;
- по катету и острому углу: катет MK = PN — по условию, ∠KMP = ∠NPM — по условию.
Автор ответа:
2
а) гипотенуза MN - общая, MK = PN. Тогда треугольники равны по гипотенузе и катету.
б) Если углы KMP = углу NPM, то угол KPM = PMN, гипотенуза MN - общая. Треугольники равны по гипотенузе и двум острым углам.
Похожие вопросы
Предмет: Русский язык,
автор: aleftina2013
Предмет: Русский язык,
автор: meteor10
Предмет: Русский язык,
автор: Миллкис
Предмет: Физика,
автор: nastasyanal
Предмет: Математика,
автор: Тимоха789