Question

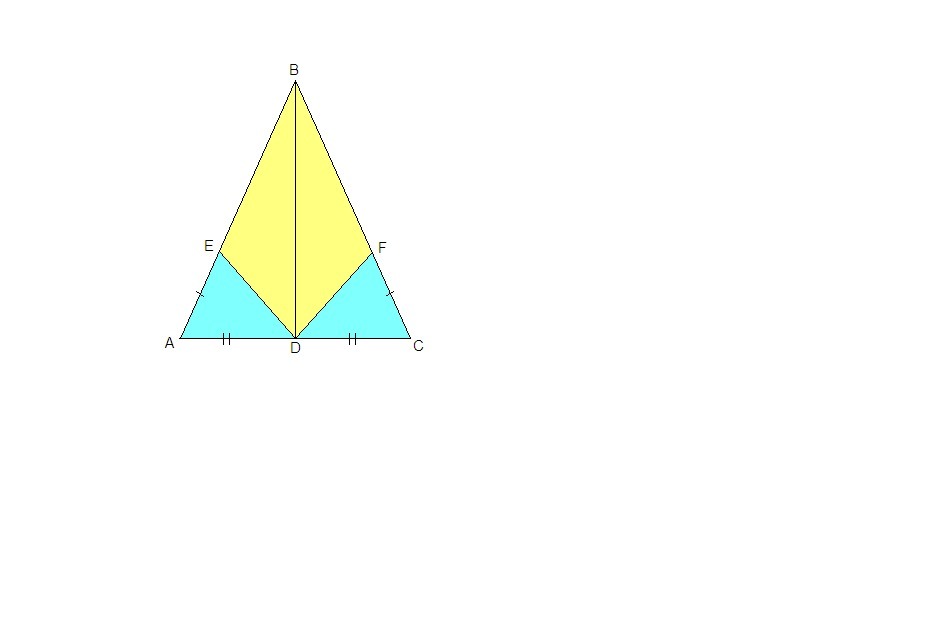
В равноедренном треугольнике ABC с основанием AC  проведена медиана BD.на сторонах AB и CB  отмечены соответственно точки E и F  так ,что   AE =CF.Докажите , что
а) треугольник BDE=треугольника BDF
б)  треуголник ADE=треугольникаCDF

Answer 1

а) ВЕ = АВ - АЕ

BF = BC - CF

АВ = ВС так как треугольник равнобедренный,

AE = CF по условию, значит

BE = BF.

∠EBD = ∠FBD так как в равнобедренном треугольнике медиана, проведенная из вершины, является биссектрисой,

BD - общая сторона для треугольников BDE и BDF, ⇒

ΔBDE = ΔBDF по двум сторонам и углу между ними.

б) DE = DF из равенства треугольников BDE и BDF,

AE = CF по условию,

AD = DC, так как BD медиана, ⇒

ΔADE = ΔCDF по трем сторонам.