Предмет: Геометрия,
автор: todor1076
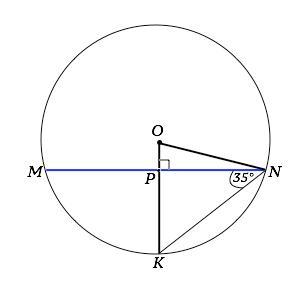
MN-хорда окружности с центром в точке О. B данной окружности проведено радиусы ON и OK, который проходит через середину отрезка MN - точку P. Угол KNP=35 градусов. Найдите углы треугольника PNO.
Ответы
Автор ответа:
2
Ответ: 90°, 20°. 70°.
Объяснение:
Радиус, проходящий через середину хорды, перпендикулярен ей. ⇒
∆ KNP и ∆ ONP прямоугольные с прямым углом при вершине Р.
Сумма острых углов прямоугольного треугольника 90°.
В ∆ KNP ∠PKN=90°-∠PNK=90°-35°=55°.
Так как ∆ КОN - равнобедренный ( ОК=ОN- радиусы), его углы ОNК=ОКN=55°
Тогда ∠ОNP=KNO-KNP=55°-35°=20°
∠РОN=90°-20°=70°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: MNikaS
Предмет: Английский язык,
автор: Berezhnoyantos
Предмет: Русский язык,
автор: lbfyecmrf2013
Предмет: Обществознание,
автор: Aaammmm