Предмет: Геометрия,
автор: std310705
Помогите пожалуйста!
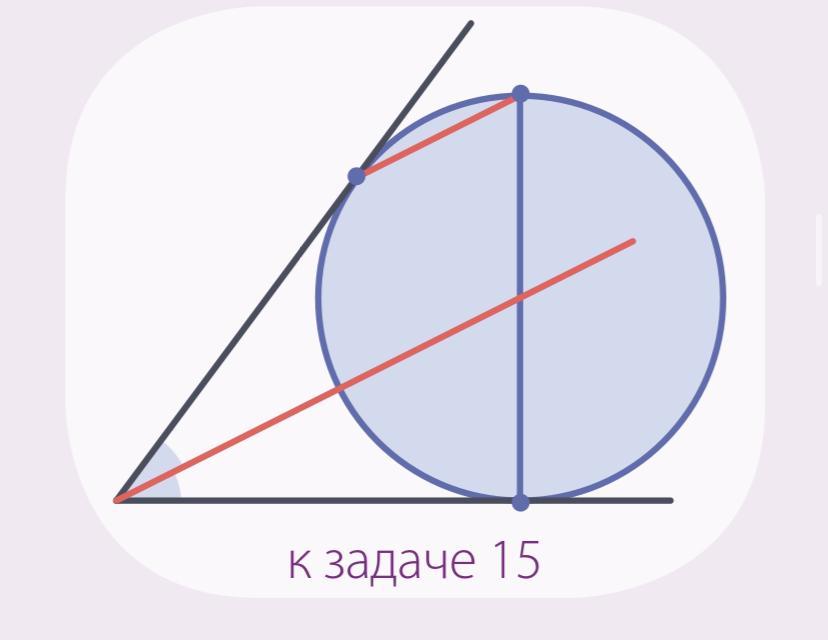
В угол вписана окружность. Через точку её касания со стороной провели диаметр. Другой конец диаметра соединили со вто рой точкой касания окружности. Докажите, что полученный отрезок параллелен бис сектрисе угла.
Приложения:
Ответы
Автор ответа:
6
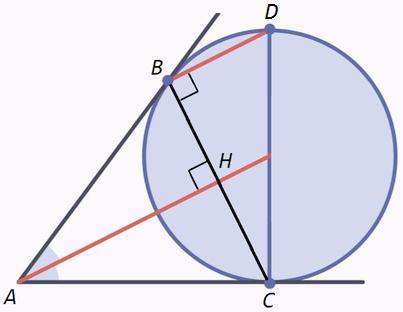
Отрезки касательных из одной точки равны, AB=AC
△BAC - равнобедренный, биссектриса является высотой, AHB=90
CBD=90 (вписанный угол, опирается на диаметр)
Накрест лежащие углы равны, AH||BD
----------------------------------
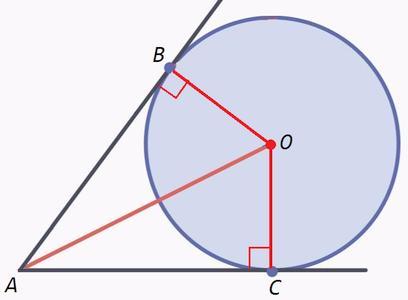
O - центр окружности, OB=OC (радиусы)
Радиус в точку касания перпендикулярен касательной.
ABO=ACO=90
△AOB=△AOC по катету и гипотенузе, AB=AC
Отрезки касательных из одной точки равны.
Приложения:
std310705:
Спасибо за решение
Можете пожалуйста помочь ещё с 2 задачами ?)
Пожалуйста))
Похожие вопросы
Предмет: Русский язык,
автор: torbarov
Предмет: Русский язык,
автор: Alexatv14
Предмет: Русский язык,
автор: Kir1006
Предмет: Информатика,
автор: Danilyk1284
Предмет: Геометрия,
автор: skavo3rodac4humi