Question

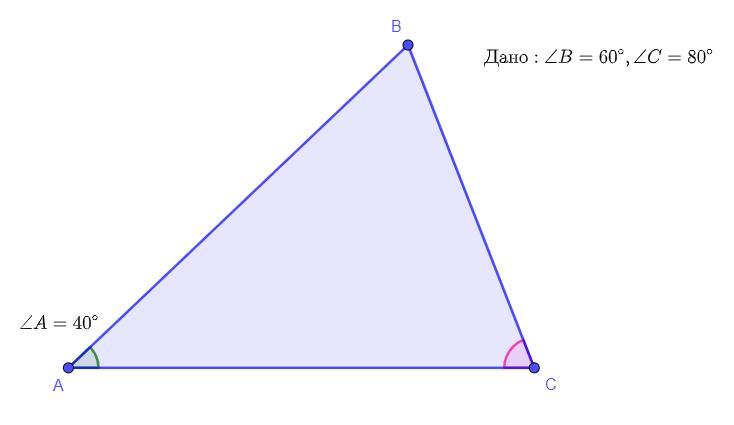
В треугольнике ABC угол B равен 60°, угол C равен 80°. Сравните отрезки BC и AB.

Answer 1

Ответ:

BC < AB

Объяснение:

Дано: ∠B = 60°, ∠C = 80°

Найти: BC ∨ AB

Решение:

По теореме про сумму углов треугольника:

∠A + ∠B + ∠C = 180° ⇒ ∠A = 180° - ∠B - ∠C =  180° - 60° - 80° = 40°

По теореме синусов:

$\boxed{ \dfrac{BC}{\sin \angle A} = \dfrac{AB}{\sin \angle C} \Longleftrightarrow \dfrac{BC}{AB} = \dfrac{\sin \angle A}{\sin \angle C}}$

Если BC > AB, то $\dfrac{BC}{AB} > 1$

Если BC < AB, то $\dfrac{BC}{AB} < 1$

Если BC = AB, то $\dfrac{BC}{AB} = 1$

$\dfrac{BC}{AB} = \dfrac{\sin \angle A}{\sin \angle C} = \dfrac{\sin 40^{\circ}}{\sin 80^{\circ}} = \dfrac{\sin 40^{\circ}}{2\sin 40^{\circ}\cos 40^{\circ}} = \dfrac{1}{2\cos 40^{\circ}}$

Функция y = cos x убывает при x ∈ [0°;90°]

$\cos 30^{\circ} = \dfrac{\sqrt{3} }{2} \approx 0,86$

$\cos 60^{\circ} = \dfrac{1}{2} = 0,5$

$\cos 30^{\circ} > \cos 40^{\circ} > \cos 60^{\circ}$

$0,86 > \cos 40^{\circ} > 0,5$

1) $\dfrac{1}{2\cos 30^{\circ}} = \dfrac{1}{2 \cdot 0,86} = \dfrac{1}{1,72} \approx 0,6 < 1$

2) $\dfrac{1}{2\cos 60^{\circ}} = \dfrac{1}{2 \cdot 0,5} = \dfrac{1}{1} = 1$

Однако, так как $\cos 40^{\circ} > 0,5$ и неравенство строгое, то выражение

$\dfrac{1}{2\cos 40^{\circ}} < 1$, таким образом BC < AB.