Предмет: Алгебра,
автор: erikabykova7
решить двумя способами!!!
1) методом выделения полного квадрата
2) по формуле корней кв. вид.
30 баллов!!
Пожалуйста, напишите решение на листке. Срочно!!
Приложения:
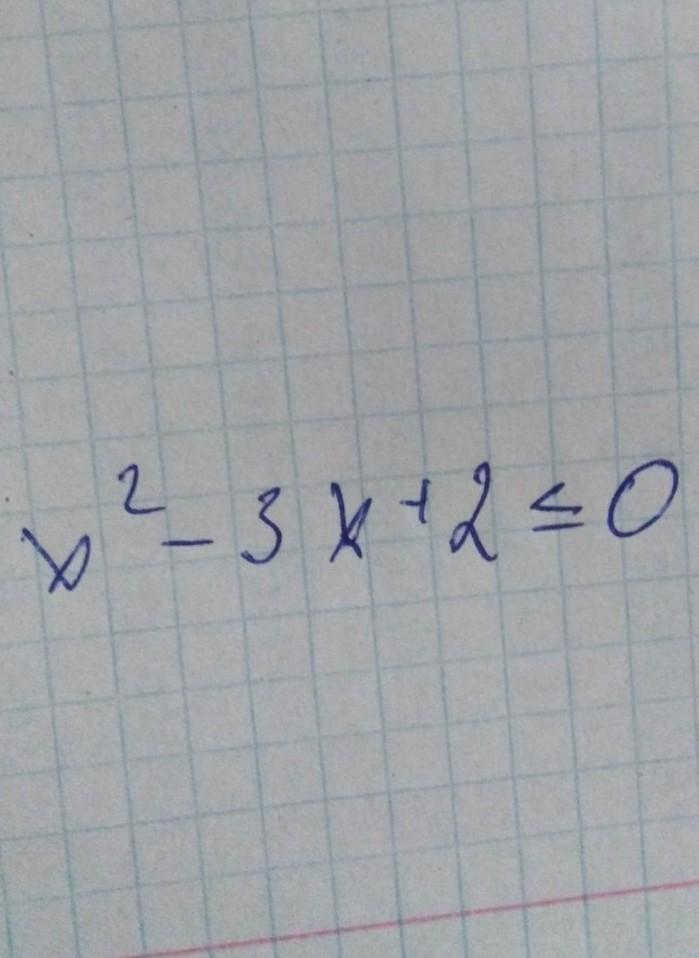
Ответы
Автор ответа:
0
Автор ответа:
1
х²-3х+2≤0
(х-1.5)²-2.25+2≤0
(х-1.5-0.5)(х-1.5+0.5)≤0
(х-2)(х-1)≤0
__1_______2________
+ - +
х∈[1;2]
можно и по Виету) третьим способом.
По формуле корней х=(3±√(9-8))/2=(3±1)/2; х=1; х=2
(х-2)(х-1)≤0
__1_______2________
+ - +
х∈[1;2]
Похожие вопросы
Предмет: Русский язык,
автор: brizgalovakrist
Предмет: Русский язык,
автор: ambassador17
Предмет: Русский язык,
автор: aleksfom
Предмет: Литература,
автор: al1gebulakas
Предмет: Алгебра,
автор: TomGlow