ДАЮ 50 БАЛОВ Два кола мають внутрішній дотик у точці А, причому менше коло
проходить через центр більшого. Доведіть, що будь-яка хорда більшого
кола, яка виходить із точки А, ділиться меншим колом навпіл.
Ответы
Два круга имеют внутреннее прикосновение в точке А, причем меньше круг проходит через центр большей. Докажите, что любая хорда большей круги, которая выходит из точки А, делится меньшим кругом пополам.
Объяснение:
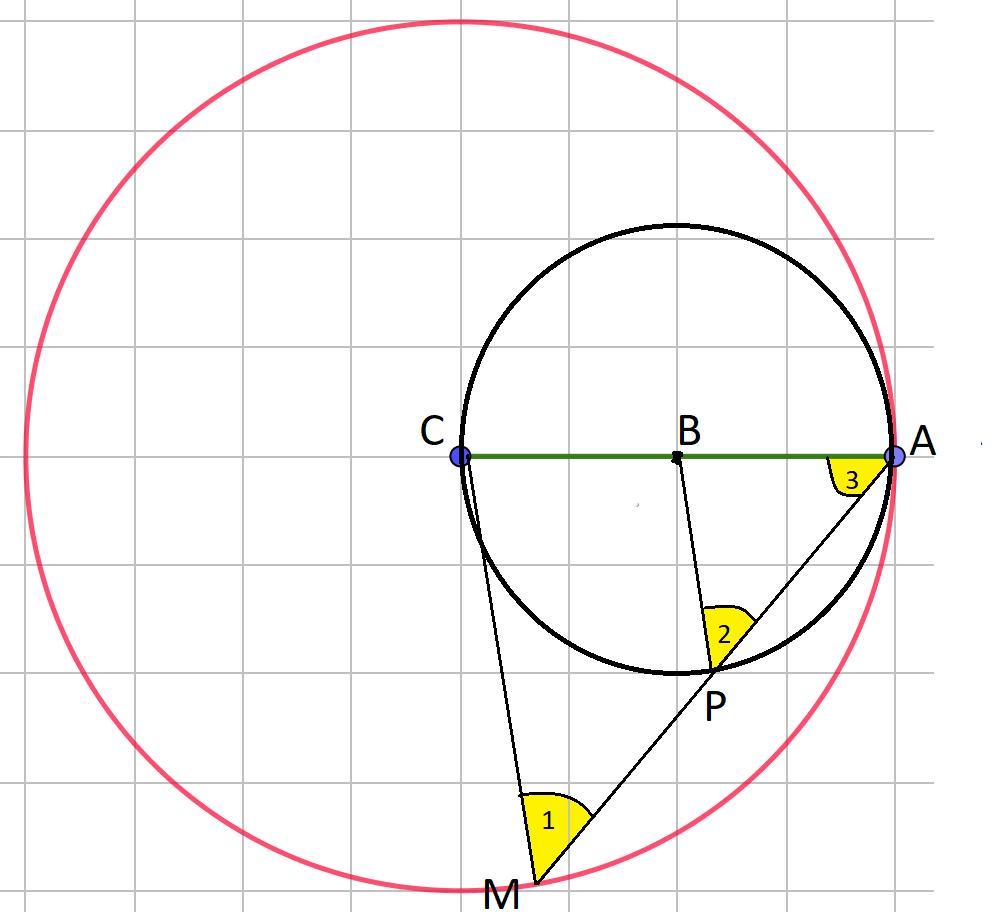
Дано:окр С(R=CA) ,окр В (r=ВА) ,СА=2ВА, внутреннее касание в точке А.
Доказать :что любая хорда большего круга, выходящая из точки А, делится меньшей окружностью пополам.
Доказательство.
Пусть АМ-хорда большей окружности , пересекает меньшую окружность в точке Р. Необходимо доказать , что Р-середина АМ или АМ=2АР.
1)ΔАМС- равнобедренный , т.к СА=СМ=R, значит ∠1=∠3.
2) ΔАРВ-равнобедренный , т.к ВА=ВР=r, значит ∠2=∠3.
ΔАМС подобен ΔАРВ по двум углам : ∠1= ∠2 , ∠3-общий . В подобных треугольниках сходственные стороны пропорциональны :
СА:ВА=АМ:АР или 2ВА:ВА=АМ:АР или 2:1=АМ:АР , АМ=2АР , значит Р-середина.