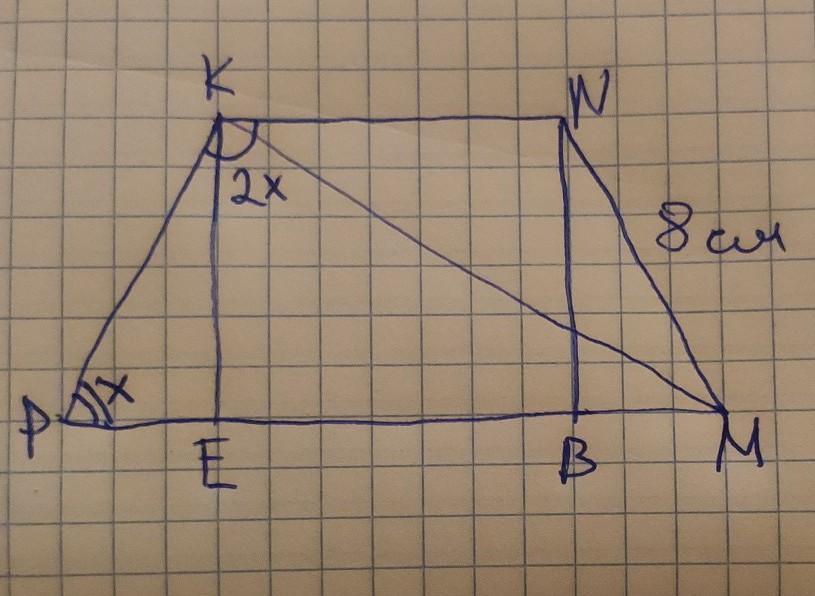
помогите пожалуйста с геометрией)

Ответы
Объяснение:
Дано:
МК —биссектриса угла NMP
NK— 8 см
Решение:
Так как трапеция равнобедренная то угол KPM= угол NMP, а угол PKN= угол MNK.
Пусть меньшие углы — угол KPM и угол NMP будет по х, тогда большие — угол PKN и угол MNK по 2х.
Найдем х.
Углы при одной бокоовой стороне трапеции в сумме дают 180°
Тогда:
Угол KNM+ угол NMP=180°
2x+x=180
3x=180
x=60
Тогда угол KPM и угол NMP по 60°, а угол PKN и угол MNK по 60°*2=120°
Рассмотрим ∆КNM
Так как КМ биссектриса угла NMP, то угол KMN=60°÷2=30°
Угол MNK=120°
Найдём угол NKM.
Сумма углов в треугольнике 180°, следовательно:
Угол NKM=180°–угол KMN–угол MNK=180°–30°–120°=30°
Получаем что ∆КNM равнобедренный с основанием КМ, следовательно NM=KN=8 см.
Рассмотрим ∆РКМ.
Так как трапеция равнобедренная её боковые стороны равны, следовательно КР=NM=8
Угол КРМ=60°
Так как КМ биссектриса угла NMP, то угол KMP=60°÷2=30°
Тогда угол PKM=180°–угол KMP–угол КРМ=180°–30°–60°=90°
Следовательно ∆РКМ прямоугольный.
По теореме если в прямоугольном треугольнике катет лежит против угла в 30°, то данный катет равен половине гипотенузы. Следовательно: PM=2*KP=2*8=16.
Проведём высоты КЕ и NB из углов PKN и KNM соответственно к стороне PM.
КNBЕ – прямоугольник так как углы KЕB и NBЕ прямые (углы образованные высотами), следовательно:
ЕB=KN=8 см
ЕК=NB
Рассмотрим треугольники ∆KЕP и ∆NBM
Угол KЕP=NBM (углы образованные высотами)
Следовательно треугольники прямоугольные
ЕК=NB;
КР=NM;
Следовательно прямоугольные треугольники равны по катету и гипотенузе.
Исходя из этого: ЕР=ВМ как соответственные катеты. Тогда ЕР+ВМ=2*ЕР
РМ=ЕВ+ЕР+ВМ=ЕВ+2*ЕР
Подставим известные значения, получим:
16=8+2*ЕР
8=2*ЕР
ЕР=4
Рассмотрим ∆КЕР.
КР=8
ЕР=4
Найдём ЕК.
По теореме Пифагора:
КР²=ЕР²+ЕК²
8²=4²+ЕК²
64=16+ЕК²
КК²=48
ЕК=√48
Sтрапеции=0,5*(а+b)*h
Где а и b основания трапеции, а h– высота.
Подставим значения:
S=0,5*(8+16)*√48=12√48=48√3 см²
КЕ делит МР в соотношении АР÷(АВ+ВМ)=4÷(16+4)=4÷20=1÷5
Ответ: S=48√3 см²; 1/5