Предмет: Геометрия,
автор: Holodev1
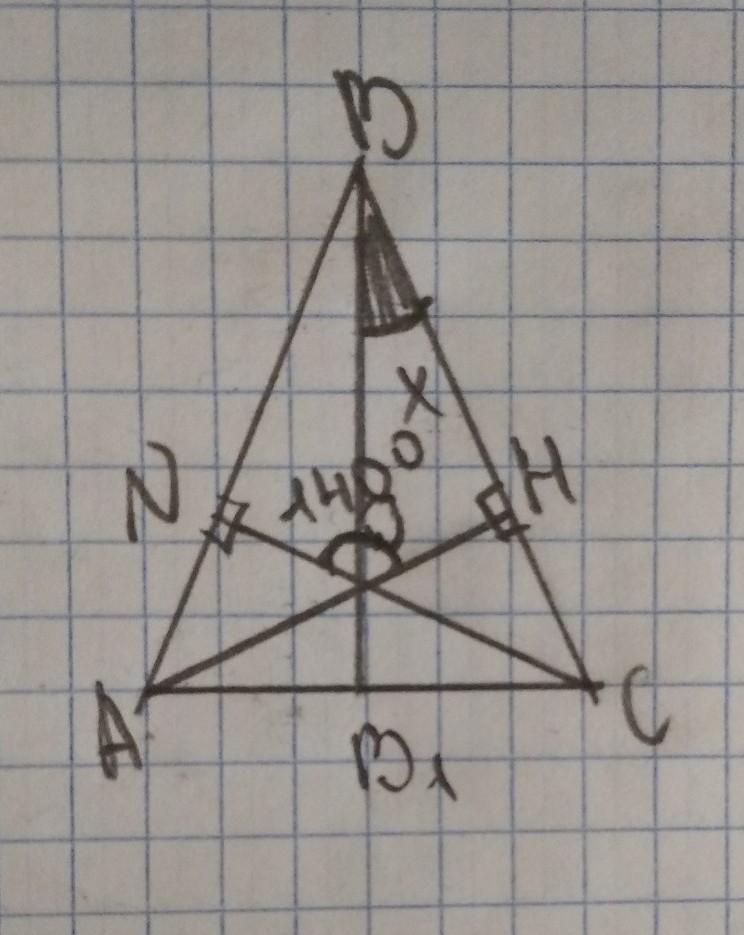
В равнобедренном треугольнике АВС с основанием АС проведены высоты АH и СN, которые пересекаются в точке О. Найдите угол CВО, если ∠HОN = 140°. Ответ дайте в градусах.
Можно с решением пожалуйста очень срочно
Ответы
Автор ответа:
12
Ответ:
20
Объяснение:
ВВ1- высота, но тк ∆равнобедренный он является ещё и биссектрисой.
из четырёхугольника ОNBH найдём угол <NBH=360°-90°-90°-140°=40°
И тк ВВ1 биссектриса, <CBO=40°:2=20°
Приложения:
Автор ответа:
9
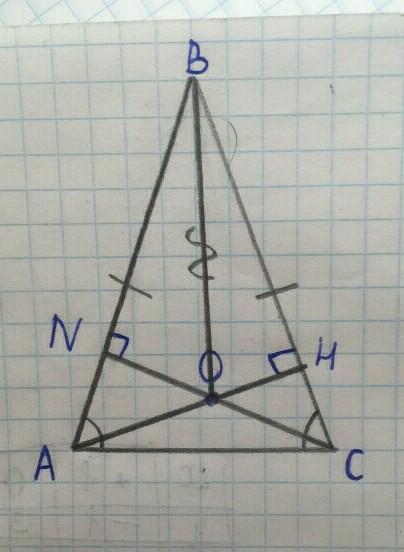
Дано:
△ABC - равнобедренный.
AC - основание.
AH и CN - высоты.
∠HON = 140˚
Найти:
∠CBO.
Решение.
Рассмотрим △BHO и △BNO:
Они прямоугольные.
BO - общая сторона.
BN = BH, т.к. △ABC - равнобедренный.
=> △BNO = △BHO, по гипотенузе и катету.
Т.к. △BNO = △BHO => ∠HOB = ∠NOB = 140 : 2 = 70˚
СУММА ОСТРЫХ углов прямоугольного треугольника равняется 90°
=> CBO = 90 - 70 = 20˚
Ответ: 20°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: marinapashkeeva
Предмет: Другие предметы,
автор: Люська555
Предмет: Русский язык,
автор: valeevdanila
Предмет: Математика,
автор: Gather
Предмет: Математика,
автор: danil663